Hình thoi là một dạng tứ giác đặc biệt, nổi bật với bốn cạnh bằng nhau. Bên cạnh những đặc điểm cơ bản, việc nắm vững kiến thức về đường Chéo Hình Thoi đóng vai trò quan trọng trong học tập và ứng dụng thực tế. Bài viết này sẽ đi sâu vào các tính chất, công thức tính toán, và bài tập vận dụng liên quan đến đường chéo của hình thoi.
Đường Chéo Của Hình Thoi Là Gì?
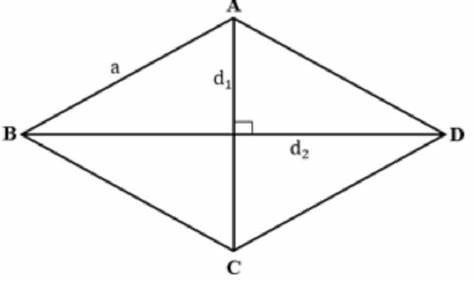
Đường chéo hình thoi là đoạn thẳng nối hai đỉnh đối diện của hình thoi. Mỗi hình thoi có hai đường chéo, chúng giao nhau tại trung điểm của mỗi đường.
Hình ảnh minh họa hai đường chéo của hình thoi cắt nhau tại trung điểm, tạo thành các góc vuông, thể hiện tính chất quan trọng của đường chéo trong hình thoi.
Tính Chất Quan Trọng Của Hai Đường Chéo Hình Thoi
Hai đường chéo của hình thoi sở hữu những tính chất đặc biệt, giúp ích rất nhiều trong việc giải toán và nhận biết hình thoi:
- Vuông góc: Hai đường chéo của hình thoi luôn vuông góc với nhau tại giao điểm. Đây là một trong những tính chất quan trọng nhất.
- Phân giác: Mỗi đường chéo là đường phân giác của các góc tại đỉnh mà nó đi qua. Nói cách khác, chúng chia các góc đó thành hai góc bằng nhau.
- Đối xứng: Mỗi đường chéo là một trục đối xứng của hình thoi. Khi gập hình thoi theo một đường chéo, hai nửa sẽ hoàn toàn trùng khít lên nhau.
Công Thức Tính Độ Dài Đường Chéo Hình Thoi
Có nhiều cách để tính độ dài đường chéo hình thoi, tùy thuộc vào thông tin đã biết. Dưới đây là một số công thức phổ biến:
-
Khi biết diện tích (S) và đường chéo còn lại (d₂):
- d₁ = (2 * S) / d₂
-
Khi biết độ dài cạnh (a) và một góc (α):
- Sử dụng định lý hàm cos trong tam giác tạo bởi một cạnh và hai nửa đường chéo.
-
Khi biết cạnh và chiều cao:
- Tính diện tích hình thoi bằng công thức: S = cạnh * chiều cao.
- Sau đó áp dụng công thức tính đường chéo khi biết diện tích và đường chéo còn lại.
Hình ảnh mô tả hình thoi với các yếu tố như cạnh, đường chéo và góc, giúp người đọc hình dung và áp dụng công thức tính đường chéo một cách trực quan.
Bài Tập Vận Dụng Tính Đường Chéo Hình Thoi
Để hiểu rõ hơn về cách áp dụng các công thức, hãy cùng xem xét một vài ví dụ sau:
Bài toán 1: Một hình thoi có diện tích 360 cm² và một đường chéo dài 24 cm. Tính độ dài đường chéo còn lại.
Giải:
- Áp dụng công thức: d₁ = (2 * S) / d₂
- d₁ = (2 * 360) / 24 = 30 cm
Bài toán 2: Một hình thoi có diện tích 4 dm² và một đường chéo dài 3/5 dm. Tính độ dài đường chéo còn lại.
Giải:
- Đổi 4 dm² = 400 cm² và 3/5 dm = 6 cm
- Áp dụng công thức: d₁ = (2 * S) / d₂
- d₁ = (2 * 400) / 6 = 133.33 cm
Bài toán 3: Hai đường chéo của hình thoi có độ dài 160 cm và 120 cm. Tính chiều cao của hình thoi, biết tỉ số giữa chiều cao và độ dài cạnh hình thoi là 24:25.
Giải:
- Diện tích hình thoi: S = (160 * 120) / 2 = 9600 cm²
- Gọi chiều cao là 24a và cạnh là 25a.
- Diện tích hình thoi: S = 24a * 25a = 600a² = 9600 cm²
- => a² = 16 => a = 4 cm
- Chiều cao của hình thoi: h = 24 * 4 = 96 cm
Hình ảnh thể hiện rõ đường cao của hình thoi, giúp người đọc hiểu rõ hơn về khái niệm và áp dụng vào các bài toán liên quan.
Tóm Tắt
Hiểu rõ về đường chéo hình thoi, các tính chất và công thức tính toán liên quan là rất quan trọng. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn tự tin hơn khi giải các bài toán về hình thoi. Việc luyện tập thường xuyên với các bài tập khác nhau sẽ giúp bạn nắm vững kiến thức và áp dụng một cách linh hoạt.