Hình vuông là một hình học cơ bản, quen thuộc trong cuộc sống hàng ngày. Để hiểu rõ hơn về hình vuông, việc nắm vững các tính chất và cách tính đường Chéo Của Hình Vuông là vô cùng quan trọng. Bài viết này sẽ cung cấp kiến thức đầy đủ và chi tiết về vấn đề này, đồng thời mở rộng ra các ứng dụng thực tế.
Tính Chất Của Hình Vuông
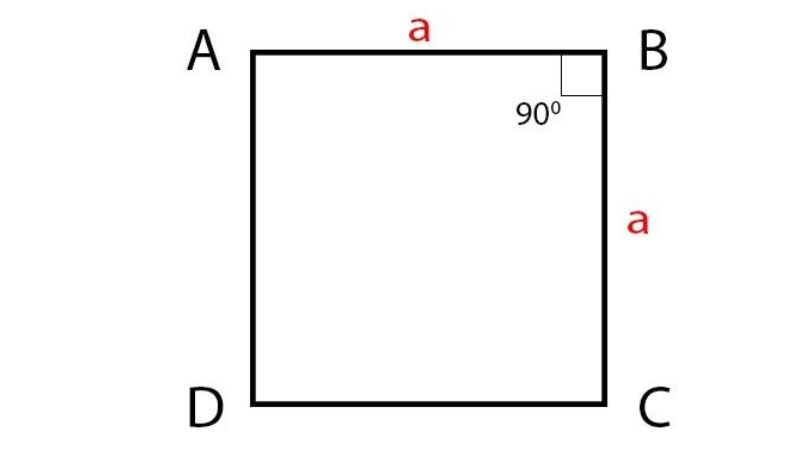
Trước khi đi sâu vào công thức tính đường chéo của hình vuông, chúng ta cần hiểu rõ các tính chất quan trọng của nó. Hình vuông là một tứ giác đều, có bốn cạnh bằng nhau và bốn góc vuông.
Hình ảnh minh họa một hình vuông ABCD, với các cạnh AB, BC, CD, DA bằng nhau và các góc tại A, B, C, D đều là góc vuông. Đường chéo AC và BD là đoạn thẳng nối hai đỉnh đối diện.
Ngoài ra, hình vuông còn sở hữu những tính chất đặc biệt sau:
- Hai đường chéo bằng nhau.
- Hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường.
- Hai đường chéo là các đường phân giác của các góc trong hình vuông.
- Hình vuông vừa là hình chữ nhật, vừa là hình thoi.
Đường Chéo Hình Vuông: Định Nghĩa và Công Thức Tính
Đường chéo của hình vuông là đoạn thẳng nối hai đỉnh đối diện của hình vuông. Đường chéo chia hình vuông thành hai tam giác vuông cân bằng nhau.
Hình ảnh này thể hiện rõ ràng cách đường chéo AC chia hình vuông ABCD thành hai tam giác vuông cân là tam giác ABC và tam giác ADC.
Để tính độ dài đường chéo của hình vuông, ta sử dụng định lý Pitago. Gọi a là độ dài cạnh của hình vuông và d là độ dài đường chéo. Khi đó, ta có:
d² = a² + a²
d² = 2a²
d = a√2Vậy, công thức tính đường chéo của hình vuông là:
d = a√2
Trong đó:
- d là độ dài đường chéo
- a là độ dài cạnh hình vuông
Bài Tập Vận Dụng
Để hiểu rõ hơn về công thức tính đường chéo của hình vuông, chúng ta hãy cùng làm một số bài tập ví dụ:
Bài tập 1: Một hình vuông có cạnh dài 5cm. Tính độ dài đường chéo của hình vuông đó.
Giải:
Áp dụng công thức d = a√2, ta có:
d = 5√2 cm
Vậy độ dài đường chéo của hình vuông là 5√2 cm (khoảng 7.07 cm).
Hình ảnh minh họa cách áp dụng định lý Pitago để tính đường chéo của hình vuông khi biết độ dài cạnh.
Bài tập 2: Một hình vuông có đường chéo dài 8cm. Tính độ dài cạnh của hình vuông đó.
Giải:
Áp dụng công thức d = a√2, suy ra a = d/√2
a = 8/√2 = 4√2 cm
Vậy độ dài cạnh của hình vuông là 4√2 cm (khoảng 5.66 cm).
Ứng Dụng Thực Tế Của Đường Chéo Hình Vuông
Việc tính toán đường chéo của hình vuông không chỉ là một bài toán hình học khô khan mà còn có rất nhiều ứng dụng thực tế trong đời sống và các lĩnh vực khác nhau.
Xây Dựng và Thiết Kế
Trong xây dựng và thiết kế, việc tính toán đường chéo của hình vuông giúp đảm bảo tính chính xác và cân đối của các công trình, từ việc bố trí cửa, cửa sổ đến việc thiết kế nội thất.
Đo Lường và Cắt Gọt
Trong đo lường và cắt gọt vật liệu, việc tính toán đường chéo của hình vuông giúp xác định kích thước và vị trí cắt một cách chính xác, đặc biệt khi cần chia hình vuông thành các phần bằng nhau.
Công Nghệ và Điện Tử
Trong lĩnh vực công nghệ và điện tử, đường chéo của hình vuông được sử dụng để tính kích thước màn hình hiển thị, thiết kế vi mạch và các thiết bị điện tử khác.
Hình ảnh cho thấy cách đường chéo của màn hình được sử dụng để xác định kích thước tổng thể của thiết bị.
Thiết Kế Đồ Họa và Nghệ Thuật
Trong thiết kế đồ họa và nghệ thuật, đường chéo của hình vuông được sử dụng để tạo sự cân đối, hài hòa và đối xứng trong các tác phẩm.
Mở Rộng: Đường Chéo Hình Chữ Nhật
Để hiểu rõ hơn về đường chéo, chúng ta cũng nên xem xét về đường chéo của hình chữ nhật. Hình chữ nhật là một tứ giác có bốn góc vuông, nhưng các cạnh đối diện có thể có độ dài khác nhau.
Hình ảnh minh họa một hình chữ nhật ABCD, với các cạnh AB và CD bằng nhau, AD và BC bằng nhau. Đường chéo AC và BD là đoạn thẳng nối hai đỉnh đối diện.
Tính chất của đường chéo hình chữ nhật:
- Hai đường chéo bằng nhau.
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Để tính độ dài đường chéo của hình chữ nhật, ta cũng sử dụng định lý Pitago. Gọi a là chiều dài và b là chiều rộng của hình chữ nhật, d là độ dài đường chéo. Khi đó, ta có:
d² = a² + b²
d = √(a² + b²)Hình ảnh minh họa cách áp dụng định lý Pitago để tính đường chéo của hình chữ nhật khi biết chiều dài và chiều rộng.
Vậy, công thức tính đường chéo của hình chữ nhật là:
d = √(a² + b²)
Kết Luận
Nắm vững kiến thức về đường chéo của hình vuông và hình chữ nhật không chỉ giúp bạn giải quyết các bài toán hình học mà còn mở ra những ứng dụng thực tế trong nhiều lĩnh vực khác nhau. Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích và thú vị.