Đường cao ứng với cạnh huyền là một khái niệm quan trọng trong hình học tam giác vuông, giúp giải quyết nhiều bài toán liên quan đến tính toán độ dài và chứng minh các hệ thức. Bài viết này sẽ hệ thống kiến thức về đường Cao ứng Với Cạnh Huyền, các hệ thức liên quan và các dạng bài tập thường gặp, giúp bạn nắm vững và áp dụng hiệu quả.
I. Các Hệ Thức Quan Trọng Về Đường Cao Ứng Với Cạnh Huyền
1. Định Lý Pytago
Định lý Pytago là nền tảng để giải quyết nhiều bài toán tam giác vuông:
- Định lý Pytago (thuận): Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Công thức: a² = b² + c² (với a là cạnh huyền, b và c là hai cạnh góc vuông). - Định lý Pytago (đảo): Nếu một tam giác có bình phương của một cạnh bằng tổng bình phương hai cạnh còn lại thì tam giác đó là tam giác vuông.
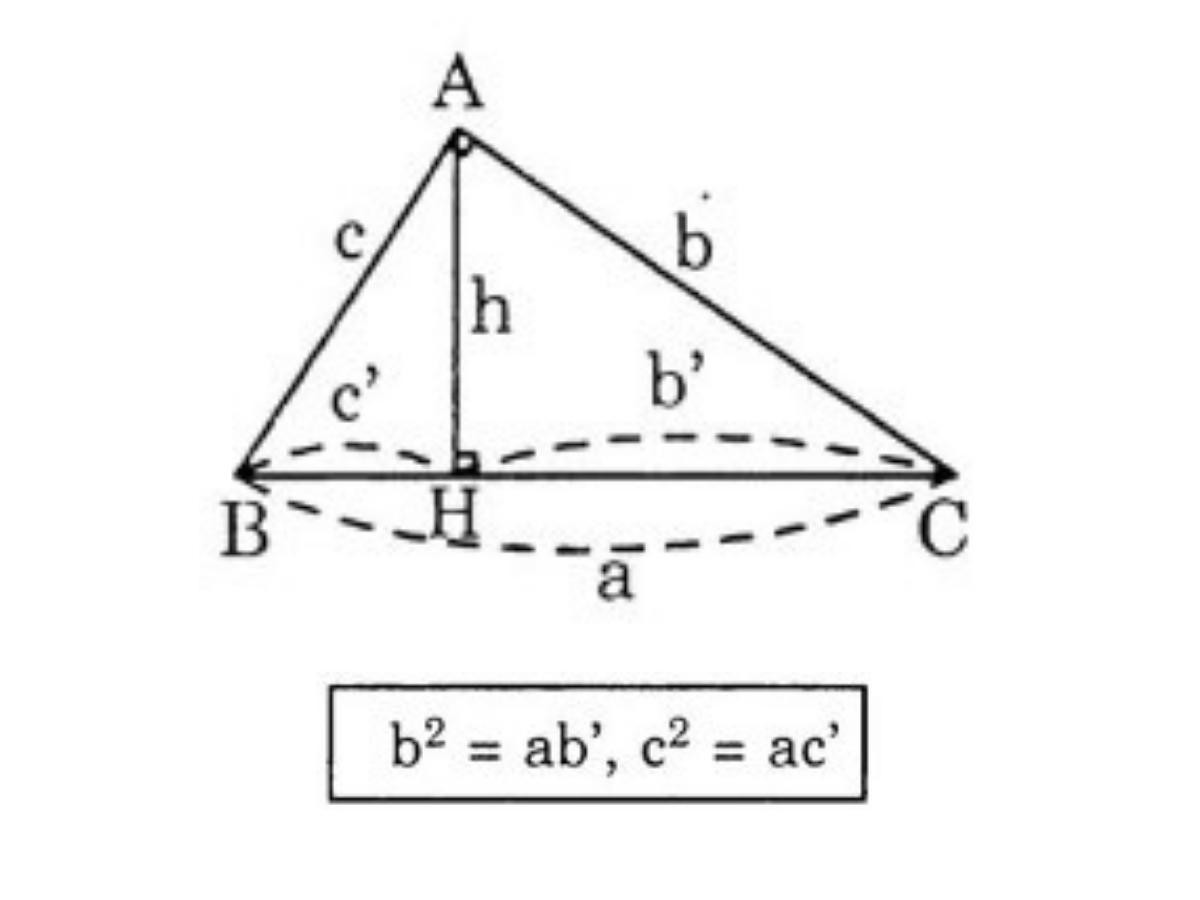
2. Hệ Thức Giữa Cạnh Góc Vuông và Hình Chiếu Trên Cạnh Huyền
Bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
3. Các Hệ Thức Liên Quan Đến Đường Cao Ứng Với Cạnh Huyền
Đây là trọng tâm của bài viết, các hệ thức này liên quan trực tiếp đến đường cao ứng với cạnh huyền:
-
Hệ thức 1: Bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
Công thức: h² = x * y (với h là đường cao, x và y là độ dài hai hình chiếu). -
Hệ thức 2: Tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng.
Công thức: a b = c h (với a, b là cạnh góc vuông, c là cạnh huyền và h là đường cao). -
Hệ thức 3: Nghịch đảo bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo bình phương hai cạnh góc vuông.
Công thức: 1/h² = 1/a² + 1/b²
II. Các Dạng Toán Thường Gặp Về Đường Cao Ứng Với Cạnh Huyền
1. Tính Độ Dài Đoạn Thẳng
Đây là dạng bài tập cơ bản, yêu cầu vận dụng các hệ thức đã nêu để tính độ dài cạnh, đường cao hoặc hình chiếu.
Ví dụ: Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Tính độ dài đường cao AH ứng với cạnh huyền BC.
Giải:
- Tính BC (cạnh huyền) theo định lý Pytago: BC² = AB² + AC² = 6² + 8² = 100 => BC = 10cm.
- Áp dụng hệ thức a b = c h: AB AC = BC AH => 6 8 = 10 AH => AH = 4.8cm.
2. Chứng Minh Hệ Thức
Dạng bài tập này yêu cầu chứng minh một hệ thức nào đó liên quan đến các yếu tố trong tam giác vuông. Thường sử dụng các phương pháp:
- Sử dụng tam giác đồng dạng: Tìm các cặp tam giác đồng dạng chứa các cạnh liên quan đến hệ thức cần chứng minh.
- Sử dụng các hệ thức về cạnh và đường cao: Biến đổi các hệ thức đã biết để suy ra hệ thức cần chứng minh.
Ví dụ: Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh rằng AB²/AC² = BH/CH.
Giải:
- Áp dụng hệ thức AB² = BH BC và AC² = CH BC.
- Suy ra AB²/AC² = (BH BC) / (CH BC) = BH/CH (đpcm).
3. Bài Toán Ứng Dụng Thực Tế
Các bài toán liên quan đến đo đạc, xây dựng, tính toán khoảng cách thường ứng dụng các kiến thức về tam giác vuông và đường cao.
III. Lời Khuyên Khi Giải Bài Toán Về Đường Cao Ứng Với Cạnh Huyền
- Vẽ hình chính xác: Việc vẽ hình rõ ràng, đầy đủ các yếu tố giúp bạn dễ dàng nhận ra các mối quan hệ và áp dụng công thức.
- Nhớ và hiểu rõ các hệ thức: Nắm vững các hệ thức là chìa khóa để giải quyết bài tập.
- Luyện tập thường xuyên: Làm nhiều bài tập giúp bạn làm quen với các dạng toán và rèn luyện kỹ năng giải.
- Phân tích đề bài kỹ lưỡng: Xác định rõ các yếu tố đã cho và yếu tố cần tìm, từ đó lựa chọn công thức phù hợp.