Đường cao là một yếu tố quan trọng trong hình học tam giác, đặc biệt là trong tam giác vuông. Bài viết này sẽ đi sâu vào khái niệm đường cao trong tam giác vuông, các công thức tính, và ứng dụng của nó thông qua các ví dụ minh họa chi tiết.
Đường Cao Trong Tam Giác Vuông Là Gì?
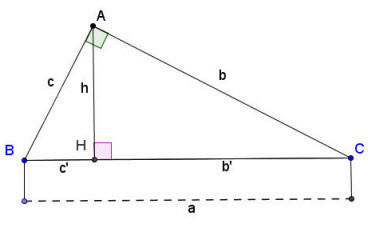
Trong tam giác vuông, đường cao là đoạn thẳng kẻ từ đỉnh góc vuông xuống cạnh huyền. Đường cao này chia tam giác vuông ban đầu thành hai tam giác vuông nhỏ đồng dạng với nhau và đồng dạng với tam giác vuông ban đầu.
Hình ảnh minh họa đường cao AH trong tam giác vuông ABC vuông tại A.
Các Công Thức Tính Đường Cao Tam Giác Vuông
Cho tam giác ABC vuông tại A, đường cao AH. Các công thức sau đây liên quan đến đường cao và các cạnh của tam giác vuông:
-
Định lý Pythagoras:
a² = b² + c²(a: cạnh huyền BC, b: cạnh góc vuông AC, c: cạnh góc vuông AB)
-
Hệ thức lượng giữa cạnh và đường cao:
b² = a * b'(b’: hình chiếu của cạnh góc vuông AC trên cạnh huyền BC)c² = a * c'(c’: hình chiếu của cạnh góc vuông AB trên cạnh huyền BC)
-
Công thức liên hệ giữa đường cao và hai cạnh góc vuông:
a * h = b * c(h: đường cao AH)
-
Công thức tính đường cao dựa trên hình chiếu:
h² = b' * c'
-
Công thức tính nghịch đảo bình phương đường cao:
1/h² = 1/b² + 1/c²
Trong đó:
- a, b, c lần lượt là độ dài các cạnh của tam giác vuông.
- b’ là hình chiếu của cạnh b (AC) trên cạnh huyền BC.
- c’ là hình chiếu của cạnh c (AB) trên cạnh huyền BC.
- h là độ dài đường cao AH.
Ví Dụ Minh Họa
Ví dụ 1: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 15cm, HC = 16cm. Tính BC, AC, AH.
Hình ảnh minh họa tam giác vuông ABC có đường cao AH, phục vụ cho việc giải bài tập.
Giải:
Áp dụng hệ thức lượng trong tam giác vuông ABC, ta có:
AC² = CH * BC = 16 * BC
Theo định lý Pythagoras:
AB² + AC² = BC²15² + 16 * BC = BC²BC² - 16 * BC - 225 = 0(BC - 25)(BC + 9) = 0
Vì BC > 0, suy ra BC = 25cm.
AC² = 16 * 25 = 400 => AC = 20cm
Xét tam giác vuông ABC:
AH * BC = AB * ACAH = (AB * AC) / BC = (15 * 20) / 25 = 12cm
Vậy BC = 25cm, AC = 20cm, AH = 12cm.
Ví dụ 2: Cho tam giác ABC vuông tại A, AB = 24cm, AC = 32cm. Đường trung trực của BC cắt AC, BC lần lượt tại D và E. Tính DE.
Hình ảnh minh họa tam giác ABC vuông tại A và đường trung trực DE của cạnh BC.
Giải:
Áp dụng định lý Pythagoras:
BC² = AB² + AC² = 24² + 32² = 1600BC = 40cm
Vì E là trung điểm của BC:
EC = BC / 2 = 20cm
Xét tam giác vuông ACB và tam giác vuông ECD:
- ∠A = ∠E = 90°
- ∠C chung
=> Tam giác ACB đồng dạng với tam giác ECD (g.g)
AC / EC = AB / EDED = (AB * EC) / AC = (24 * 20) / 32 = 15cm
Vậy ED = 15cm.
Ứng Dụng Thực Tế
Các công thức và kiến thức về đường cao trong tam giác vuông có nhiều ứng dụng trong thực tế, ví dụ như:
- Xây dựng: Tính toán chiều cao của các công trình dựa trên góc và khoảng cách.
- Thiết kế: Xác định kích thước và hình dạng tối ưu cho các cấu trúc.
- Đo đạc: Tính toán khoảng cách và diện tích trong địa lý và bản đồ.
Kết Luận
Hiểu rõ về đường cao trong tam giác vuông, các công thức liên quan và ứng dụng của nó là rất quan trọng trong học tập và giải quyết các bài toán hình học. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và cần thiết.