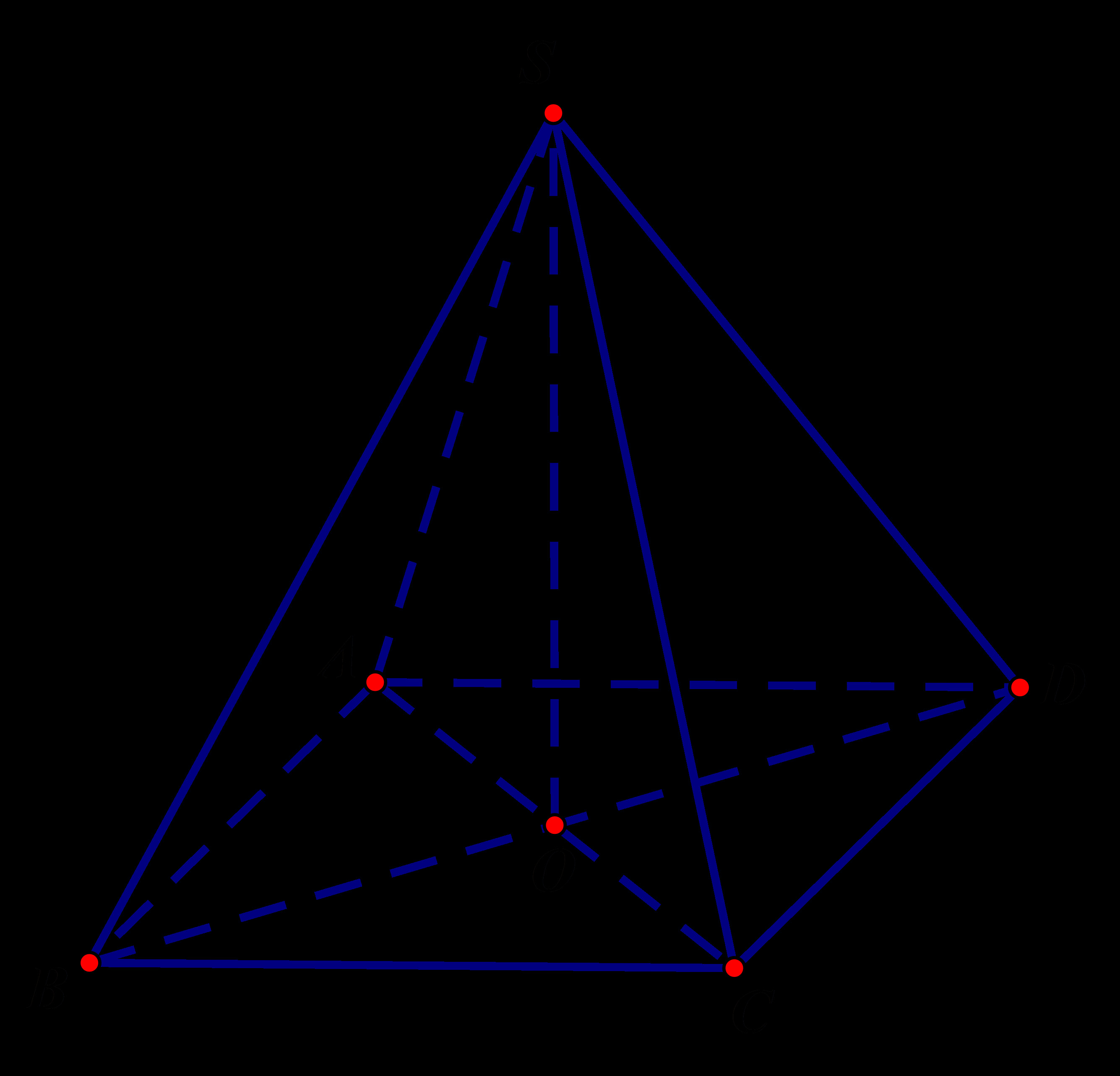
Trong hình học không gian, hình chóp đều là một hình khối quan trọng và thường gặp. Để giải quyết các bài toán liên quan đến hình chóp đều, việc nắm vững kiến thức về “đường Cao Hình Chóp đều” là vô cùng cần thiết. Bài viết này sẽ cung cấp một cái nhìn toàn diện về đường cao của hình chóp đều, từ định nghĩa, tính chất đến các ứng dụng trong tính toán và bài tập.
Hình Chóp Đều Là Gì?
Hình chóp đều là hình chóp có đáy là một đa giác đều và chân đường cao của hình chóp trùng với tâm của đa giác đáy. Tâm của đa giác đều là điểm đồng quy của các đường trung trực của các cạnh.
Đường Cao Hình Chóp Đều
Đường cao của hình chóp đều là đoạn thẳng nối từ đỉnh của hình chóp xuống mặt đáy và vuông góc với mặt đáy đó. Trong hình chóp đều, đường cao luôn đi qua tâm của đa giác đáy.
Tính Chất Quan Trọng
- Vị trí: Đường cao hình chóp đều luôn đi qua tâm của đa giác đáy.
- Vuông góc: Đường cao vuông góc với mặt phẳng chứa đáy.
- Tính đối xứng: Đường cao là trục đối xứng của hình chóp đều.
Đường Cao Trong Hình Chóp Tứ Giác Đều
Hình chóp tứ giác đều là một trường hợp đặc biệt của hình chóp đều, có đáy là hình vuông.
Tính chất của hình chóp tứ giác đều:
- Đáy là hình vuông.
- Các cạnh bên bằng nhau.
- Đường cao đi qua giao điểm của hai đường chéo hình vuông (tâm đáy).
- Các mặt bên là các tam giác cân bằng nhau.
- Các góc tạo bởi cạnh bên và mặt đáy bằng nhau.
Xác Định Đường Cao
Để xác định đường cao trong hình chóp tứ giác đều, ta thực hiện các bước sau:
- Xác định tâm của hình vuông đáy (giao điểm của hai đường chéo).
- Nối đỉnh của hình chóp với tâm của hình vuông đáy. Đoạn thẳng này chính là đường cao của hình chóp tứ giác đều.
Ứng Dụng Của Đường Cao Trong Tính Toán
Đường cao hình chóp đều đóng vai trò quan trọng trong việc tính toán thể tích và diện tích của hình chóp.
Tính Thể Tích
Thể tích của hình chóp đều được tính theo công thức:
V = (1/3) * S_đáy * hTrong đó:
V: Thể tích hình chóp.S_đáy: Diện tích đáy của hình chóp.h: Chiều cao của hình chóp (độ dài đường cao).
Tính Diện Tích Xung Quanh và Toàn Phần
Để tính diện tích xung quanh của hình chóp đều, ta cần biết độ dài trung đoạn (đường cao của mặt bên) và chu vi đáy.
-
Diện tích xung quanh:
S_xq = (1/2) * P_đáy * dTrong đó:
S_xq: Diện tích xung quanh.P_đáy: Chu vi đáy.d: Độ dài trung đoạn.
- Diện tích toàn phần:
S_tp = S_xq + S_đáy
Bài Tập Ví Dụ
Ví dụ 1: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = a và cạnh bên SA = a. Tính thể tích khối chóp S.ABCD.
Giải:
- Tính diện tích đáy:
S_ABCD = a^2 - Gọi H là tâm của hình vuông ABCD. Tính độ dài đường cao SH:
AH = (a√2)/2SH = √(SA^2 - AH^2) = √(a^2 - (a^2/2)) = (a√2)/2
- Tính thể tích:
V = (1/3) * S_ABCD * SH = (1/3) * a^2 * (a√2)/2 = (a^3√2)/6
Ví dụ 2: Cho hình chóp tứ giác đều có tất cả các cạnh bằng a. Tính thể tích khối chóp.
Giải:
- Tính diện tích đáy:
S_ABCD = a^2 - Gọi O là tâm của hình vuông ABCD. Tính độ dài đường cao SO:
OB = (a√2)/2SO = √(SB^2 - OB^2) = √(a^2 - (a^2/2)) = (a√2)/2
- Tính thể tích:
V = (1/3) * S_ABCD * SO = (1/3) * a^2 * (a√2)/2 = (a^3√2)/6
Ví dụ 3: Cho hình chóp tứ giác đều có cạnh đáy bằng x. Diện tích xung quanh gấp đôi diện tích đáy. Tính thể tích khối chóp.
Giải:
- Tính diện tích đáy:
S_đáy = x^2 - Tính diện tích xung quanh:
S_xq = 2x^2 - Gọi I là trung điểm của CD. Tính độ dài trung đoạn SI:
S_xq = 4 * (1/2) * x * SI = 2x * SI2x * SI = 2x^2 => SI = x
- Gọi O là tâm của hình vuông ABCD. Tính độ dài đường cao SO:
OI = x/2SO = √(SI^2 - OI^2) = √(x^2 - (x^2/4)) = (x√3)/2
- Tính thể tích:
V = (1/3) * S_đáy * SO = (1/3) * x^2 * (x√3)/2 = (x^3√3)/6
Kết Luận
Nắm vững kiến thức về đường cao hình chóp đều là yếu tố then chốt để giải quyết các bài toán liên quan đến hình chóp. Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và chi tiết về đường cao hình chóp đều, từ đó giúp bạn tự tin hơn trong học tập và giải quyết các bài toán hình học không gian.