Đường cao AH trong tam giác là một yếu tố quan trọng, xuất hiện thường xuyên trong các bài toán hình học. Bài viết này sẽ cung cấp cho bạn kiến thức toàn diện về đường Cao Ah, từ định nghĩa, tính chất đến các công thức tính toán trong các loại tam giác khác nhau.
Định Nghĩa Đường Cao AH trong Tam Giác
Đường cao AH của tam giác là đoạn thẳng kẻ từ đỉnh A và vuông góc với cạnh đối diện (cạnh BC). Điểm H là chân đường cao, và cạnh BC là đáy tương ứng với đường cao AH. Độ dài đoạn AH chính là khoảng cách từ đỉnh A đến đường thẳng chứa cạnh BC.
Tính Chất Quan Trọng Của Đường Cao AH
Một tính chất then chốt của đường cao AH là ba đường cao của một tam giác (kẻ từ ba đỉnh khác nhau) luôn đồng quy tại một điểm. Điểm này được gọi là trực tâm của tam giác. Trực tâm có vai trò quan trọng trong nhiều bài toán và chứng minh hình học.
Công Thức Tính Đường Cao AH trong Các Loại Tam Giác
1. Đường Cao AH trong Tam Giác Thường
Trong tam giác thường ABC, đường cao AH có thể được tính bằng công thức Heron:
Trong đó:
a,b,clà độ dài các cạnh của tam giác ABC.halà độ dài đường cao AH kẻ từ đỉnh A xuống cạnh BC.plà nửa chu vi của tam giác:p = (a + b + c) / 2.
Ví dụ: Cho tam giác ABC có AB = 4 cm, BC = 7 cm, AC = 5 cm. Tính đường cao AH.
Giải:
Nửa chu vi tam giác: p = (4 + 7 + 5) / 2 = 8 cm.
Áp dụng công thức Heron:
=> AH = 4√8 (cm)
Diện tích tam giác ABC là: SABC = (1/2) AH BC = (1/2) 4√8 7 = 14√8 (cm2).
2. Đường Cao AH trong Tam Giác Đều
Trong tam giác đều ABC có cạnh bằng a, đường cao AH được tính bằng công thức:
Trong đó:
hlà độ dài đường cao AH.alà độ dài cạnh của tam giác đều.
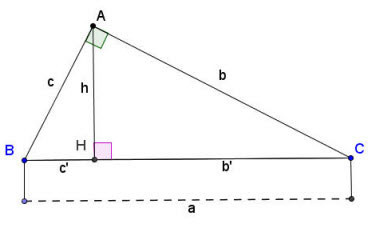
3. Đường Cao AH trong Tam Giác Vuông
Xét tam giác vuông ABC vuông tại A, đường cao AH được kẻ từ đỉnh A xuống cạnh huyền BC. Các công thức liên quan:
a² = b² + c²(Định lý Py-ta-go)b² = a.b'vàc² = a.c'(Hệ thức lượng)a.h = b.c(Hệ thức lượng)h² = b'.c'(Hệ thức lượng)1/h² = 1/b² + 1/c²
Trong đó:
a,b,clà độ dài các cạnh của tam giác vuông.b'là hình chiếu của cạnhbtrên cạnh huyền.c'là hình chiếu của cạnhctrên cạnh huyền.hlà độ dài đường cao AH.
Ví dụ 1: Cho tam giác ABC vuông tại A, đường cao AH. Tính BC, AC, AH biết AB = 15cm, HC = 16cm.
Giải:
Áp dụng hệ thức lượng trong tam giác vuông ABC có:
AC² = CH.BC = 16.BC
Theo định lí Pythagore cho tam giác ABC vuông tại A ta có:
AB² + AC² = BC²
⇔ 15² + 16.BC = BC²
⇔ BC² – 16.BC – 225 = 0
⇔ BC² – 25.BC + 9.BC – 225 = 0
⇔ BC(BC – 25) + 9(BC – 25) = 0
⇔ (BC – 25)(BC + 9) = 0
⇔ BC = 25 hoặc BC = -9 (loại)
⇒ AC² = 16.BC = 16.25 = 400 ⇒ AC = 20 (cm)
Xét tam giác vuông ABC có: AH.BC = AB.AC (hệ thức lượng)
=> AH = AB.AC/BC = 15.20/25 = 12(cm)
Vậy BC=25(cm); AC=20(cm); AH=12(cm)
Ví dụ 2: Cho tam giác ABC vuông tại A, AB=24cm, AC=32cm. Đường trung trực của BC cắt AC, BC theo thứ tự D và E. Tính DE.
Giải:
Xét tam giác vuông ABC, ta có:
BC² = AB²+ AC² ( theo định lý py-ta-go)
BC² = 24²+ 32²
BC² = 1600
BC = 40(cm)
EC = BC : 2 = 40 : 2 = 20(cm)
Xét tam giác vuông ACB và tam giác vuông ECD có:
Có ∠A = ∠E = 90°
∠C chung
=> Tam giác ACB ∾ tam giác ECD (g.g)
=> AC/EC = AB/ED
=> ED = AB.EC/AC = 15cm
Vậy ED = 15cm
4. Đường Cao AH trong Tam Giác Cân
Giả sử tam giác ABC cân tại A, đường cao AH vuông góc với BC tại H. Vì tam giác ABC cân tại A, đường cao AH đồng thời là đường trung tuyến. Do đó:
HB = HC = BC / 2
Áp dụng định lý Pytago trong tam giác vuông ABH:
AH² + BH² = AB²
=> AH² = AB² - BH²
Ví dụ: Cho Δ ABC cân tại A có BC = 30(cm), đường cao AH = 20(cm). Tính đường cao ứng với cạnh bên của tam giác cân đó.
Giải: Xét Δ ABC cân tại A có BC = 30(cm)
⇒ BH = CH = 15(cm).
Áp dụng định lý Py – ta – go ta có:
Kẻ BK vuông góc AC, giờ ta phải tính BK = ?
Ta có:
Mặt khác
Do đó, ta có ⇔
Kết Luận
Nắm vững các công thức và tính chất liên quan đến đường cao AH sẽ giúp bạn giải quyết các bài toán hình học một cách hiệu quả hơn. Hy vọng bài viết này đã cung cấp cho bạn kiến thức hữu ích về đường cao AH trong tam giác.