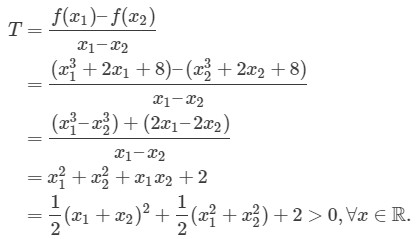Hàm số đồng biến và nghịch biến là một trong những khái niệm quan trọng trong chương trình Toán lớp 10. Việc nắm vững kiến thức này sẽ giúp học sinh giải quyết tốt các bài toán liên quan và tạo nền tảng vững chắc cho các lớp học cao hơn. Bài viết này sẽ cung cấp đầy đủ lý thuyết, phương pháp giải, ví dụ minh họa và bài tập tự luyện chi tiết về hàm số đồng Biến Nghịch Biến Lớp 10.
1. Định Nghĩa Hàm Số Đồng Biến Nghịch Biến Lớp 10
1.1. Hàm Số Là Gì?
Hàm số là một quy tắc cho tương ứng mỗi giá trị của biến số x trong một tập hợp xác định D với một và chỉ một giá trị của biến số y. Ký hiệu: y = f(x), trong đó x là biến số độc lập, y là biến số phụ thuộc, và D là tập xác định của hàm số. Tập xác định đóng vai trò quan trọng trong việc xét tính đồng biến, nghịch biến của hàm số.
1.2. Định Nghĩa Hàm Số Đồng Biến và Nghịch Biến
Cho hàm số y = f(x) xác định trên khoảng (a; b):
- Hàm số đồng biến (tăng) trên khoảng (a; b) khi và chỉ khi với mọi x1, x2 thuộc (a; b) và x1 < x2 thì f(x1) < f(x2).
- Hàm số nghịch biến (giảm) trên khoảng (a; b) khi và chỉ khi với mọi x1, x2 thuộc (a; b) và x1 < x2 thì f(x1) > f(x2).
- Hàm số không đổi (hàm hằng) trên khoảng (a; b) nếu f(x) = const với mọi x thuộc (a; b).
Công thức tổng quát về hàm số đồng biến nghịch biến.
Lưu ý:
- Đồ thị hàm số đồng biến trên một khoảng sẽ đi lên từ trái sang phải trên khoảng đó.
- Đồ thị hàm số nghịch biến trên một khoảng sẽ đi xuống từ trái sang phải trên khoảng đó.
- Hàm số bậc nhất y = ax + b (a ≠ 0) luôn đồng biến hoặc nghịch biến trên toàn bộ tập xác định của nó.
2. Phương Pháp Xét Tính Đồng Biến, Nghịch Biến Của Hàm Số Lớp 10
2.1. Phương Pháp Giải
Phương pháp 1: Sử dụng định nghĩa
- Chọn x1, x2 bất kỳ thuộc khoảng K (tập đang xét) sao cho x1 < x2.
- Tính f(x1) và f(x2).
- So sánh f(x1) và f(x2) để kết luận:
- Nếu f(x1) < f(x2) thì hàm số đồng biến trên K.
- Nếu f(x1) > f(x2) thì hàm số nghịch biến trên K.
Phương pháp 2: Xét dấu tỉ số biến thiên
-
Tính tỉ số T = (f(x2) – f(x1)) / (x2 – x1), với x1 ≠ x2 và x1, x2 thuộc K.
-
Xét dấu của T:
- Nếu T > 0 thì hàm số đồng biến trên K.
- Nếu T < 0 thì hàm số nghịch biến trên K.
Công thức tính và xét dấu tỉ số biến thiên để xác định tính đồng biến, nghịch biến của hàm số.
2.2. Ví Dụ Minh Họa
Ví dụ 1: Xét tính đồng biến và nghịch biến của hàm số $y = sqrt{1 – 2x}$ trên khoảng $(-infty; frac{1}{2}]$.
Hướng dẫn giải:
Áp dụng phương pháp 1 sử dụng định nghĩa:
Bài giải chi tiết ví dụ 1 về hàm số nghịch biến.
Kết luận: Hàm số nghịch biến trên $(-infty; frac{1}{2}]$.
Ví dụ 2: Xét tính đồng biến, nghịch biến của hàm số y = f(x) = x + 3.
Hướng dẫn giải: Áp dụng công thức tỉ số dấu (phương pháp 2):
- Tập xác định: D = R
- Với mọi x1, x2 thuộc R và x1 ≠ x2:
Kết luận: Hàm số đồng biến trên R.
Ví dụ 3: Xét sự biến thiên của hàm số $y = f(x) = frac{3x + 1}{x – 2}$ trên khoảng $(-infty; 2)$ và $(2; +infty)$.
Hướng dẫn giải:
Áp dụng phương pháp 2, xét tỉ số biến thiên:
Bài giải chi tiết ví dụ 3 về hàm số nghịch biến trên các khoảng xác định.
Kết luận: Hàm số nghịch biến trên các khoảng $(-infty; 2)$ và $(2; +infty)$.
3. Bài Tập Về Hàm Số Đồng Biến Nghịch Biến Lớp 10
Bài 1: Xét sự biến thiên của các hàm số sau trên khoảng $(1; +infty)$:
a) $y = frac{3}{x – 1}$
b) $y = frac{x + 1}{x}$
Hướng dẫn giải:
a) Với x1, x2 thuộc (1; +∞) và x1 ≠ x2:
Kết luận: Hàm số $y = frac{3}{x – 1}$ nghịch biến trên $(1; +infty)$.
b) Với x1, x2 thuộc (1; +∞) và x1 ≠ x2:
Bài giải chi tiết bài tập 1b về hàm số nghịch biến.
Bài 2: Khảo sát sự biến thiên của hàm số $y = sqrt{4x + 5} + sqrt{x – 1}$ trên tập xác định của nó.
Hướng dẫn giải:
Kết luận: Hàm số $y = sqrt{4x + 5} + sqrt{x – 1}$ đồng biến trên khoảng $[1; +infty)$.
Bài 3: Xét tính đơn điệu của hàm số $y = f(x) = x^2 – 4$ trên khoảng $(-infty; 0)$.
Hướng dẫn giải:
Bài giải chi tiết bài tập 3 về tính đơn điệu của hàm số.
Bài 4: Cho hàm số y = f(x) có đồ thị như hình vẽ dưới. Xét tính đồng biến nghịch biến của hàm số trên khoảng (2; 4) và trên đoạn [-4; -2].
Hướng dẫn giải:
- Trên khoảng (2; 4), đồ thị hàm số đi lên => Hàm số đồng biến.
- Trên đoạn [-4; -2], đồ thị hàm số đi xuống => Hàm số nghịch biến.
Bài 5: Xác định m để các hàm số sau:
a) $y = frac{mx – 4}{x – m}$ đồng biến trên từng khoảng xác định.
b) $y = -x^3 + mx^2 – 3x + 4$ nghịch biến trên R.
Hướng dẫn giải:
Hy vọng với những kiến thức và bài tập trên, các em học sinh lớp 10 sẽ nắm vững hơn về hàm số đồng biến và nghịch biến. Chúc các em học tốt!