1. Đơn thức là gì?
Đơn thức là một biểu thức đại số đơn giản, chỉ bao gồm một số, một biến, hoặc tích của các số và các biến. Ví dụ về đơn thức bao gồm: 5, x, 3xy, -2x²y³.
Để hiểu rõ hơn, hãy nhớ rằng đơn thức không chứa các phép toán cộng hoặc trừ giữa các thành phần của nó.
1.1 Đơn thức thu gọn
Để đơn giản hóa, chúng ta thường làm việc với đơn thức thu gọn. Một đơn thức thu gọn chỉ bao gồm tích của một số (hệ số) với các biến, mỗi biến chỉ xuất hiện một lần duy nhất dưới dạng lũy thừa với số mũ nguyên dương.
Ví dụ: 7x²yz là một đơn thức thu gọn, trong khi 3xyx không phải là đơn thức thu gọn vì biến x xuất hiện hai lần.
1.2 Hệ số và phần biến
Trong một đơn thức thu gọn, phần số được gọi là hệ số, và phần còn lại (tích của các biến) được gọi là phần biến.
Ví dụ: Trong đơn thức 5x²y, hệ số là 5 và phần biến là x²y.
1.3 Bậc của đơn thức
Bậc của một đơn thức thu gọn (với hệ số khác 0) là tổng số mũ của tất cả các biến trong đơn thức đó.
Ví dụ: Đơn thức 2xy có bậc là 2 (1 + 1), đơn thức 3x²y³z có bậc là 6 (2 + 3 + 1). Lưu ý rằng một số thực khác 0 là đơn thức bậc 0, và số 0 được coi là đơn thức không có bậc.
1.4 Đơn thức đồng dạng
Hai đơn thức được gọi là đồng dạng nếu chúng có hệ số khác 0 và có cùng phần biến.
Ví dụ: 4x²y và -2x²y là hai đơn thức đồng dạng, trong khi 3xy² và 3x²y không đồng dạng.
1.5 Phép toán với đơn thức đồng dạng
Chỉ có các đơn thức đồng dạng mới có thể cộng hoặc trừ trực tiếp với nhau. Để cộng (hoặc trừ) các đơn thức đồng dạng, ta cộng (hoặc trừ) các hệ số của chúng và giữ nguyên phần biến.
Ví dụ:
2x²y + 5x²y = 7x²y
8xy³ – 3xy³ = 5xy³
2. Đa thức: Tổng hợp của đơn thức
Đa thức là một biểu thức đại số được tạo thành bằng cách cộng hoặc trừ các đơn thức. Mỗi đơn thức trong đa thức được gọi là một hạng tử.
Lưu ý: Một đơn thức cũng có thể được coi là một đa thức (chỉ chứa một hạng tử). Số 0 được gọi là đa thức không.
Ví dụ: x² + 2x – 3, 4xy – y² + 5, và 7x là các đa thức.
2.1 Đa thức thu gọn
Đa thức thu gọn là một đa thức mà trong đó không có hai hạng tử nào đồng dạng. Để thu gọn một đa thức, ta cần nhóm các hạng tử đồng dạng và thực hiện phép cộng hoặc trừ để kết hợp chúng thành một hạng tử duy nhất.
Ví dụ: Đa thức x² + 3xy – xy + y² có thể được thu gọn thành x² + 2xy + y².
2.2 Bậc của đa thức
Bậc của một đa thức là bậc cao nhất của bất kỳ hạng tử nào trong đa thức đó (sau khi đã thu gọn).
Ví dụ: Đa thức x³ + 2x²y – 5y có bậc là 3 (do hạng tử x³ có bậc cao nhất).
2.3 Tính giá trị của đa thức
Để tính giá trị của một đa thức tại một giá trị cụ thể của biến, ta thay giá trị đó vào biểu thức và thực hiện các phép tính.
Ví dụ: Giá trị của đa thức x² – 3x + 2 tại x = 1 là: (1)² – 3(1) + 2 = 0.
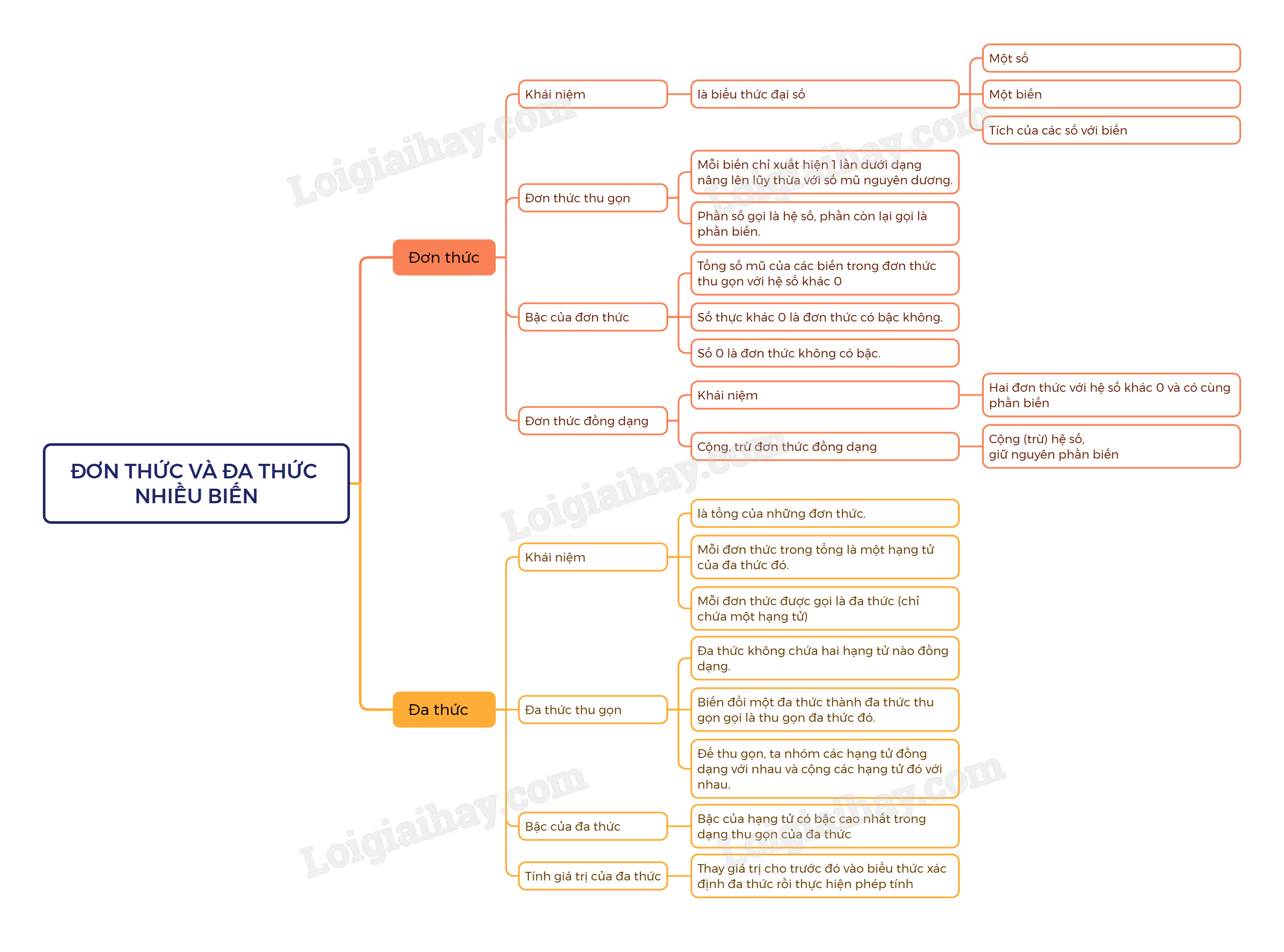
Hình ảnh minh họa các thành phần cơ bản của đơn Thức Và đa Thức, bao gồm biến, hệ số và lũy thừa, giúp học sinh dễ dàng hình dung và nắm bắt khái niệm.
Ứng dụng của đơn thức và đa thức
Đơn thức và đa thức là nền tảng cơ bản của đại số và có rất nhiều ứng dụng trong toán học, khoa học và kỹ thuật. Chúng được sử dụng để mô hình hóa các hiện tượng thực tế, giải các bài toán, và xây dựng các công thức và phương trình. Ví dụ, đa thức có thể được sử dụng để mô tả quỹ đạo của một vật thể, tính diện tích và thể tích, hoặc phân tích dữ liệu thống kê. Hiểu rõ về đơn thức và đa thức là rất quan trọng để thành công trong các lĩnh vực này.

