Hàm số y = sinx là một trong những hàm số lượng giác cơ bản và quan trọng nhất trong toán học. Việc hiểu rõ về đồ thị của hàm số này không chỉ giúp chúng ta giải quyết các bài toán liên quan mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực khoa học và kỹ thuật. Bài viết này sẽ cung cấp một cái nhìn toàn diện về đồ thị hàm số y = sinx, bao gồm các tính chất, cách vẽ và các biến thể thường gặp.
Đồ Thị Hàm Số y = sinx
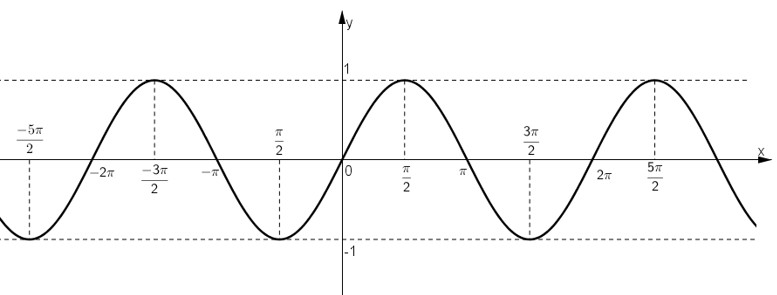
Đồ thị của hàm số y = sinx là một đường cong liên tục, lặp đi lặp lại, được gọi là đường sin. Nó thể hiện sự biến thiên của giá trị sin của một góc khi góc đó thay đổi.
Đồ thị hàm số y = sinx thể hiện trên trục tọa độ Oxy, với trục hoành biểu diễn giá trị x (thường là radian) và trục tung biểu diễn giá trị y = sinx, cho thấy sự biến thiên tuần hoàn của hàm số.
Các Tính Chất Quan Trọng của Hàm Số y = sinx
- Tập xác định: D = R (tất cả các số thực). Điều này có nghĩa là hàm số sinx được xác định cho mọi giá trị của x.
- Tập giá trị: T = [-1; 1]. Giá trị của sinx luôn nằm trong khoảng từ -1 đến 1.
- Tính tuần hoàn: Hàm số y = sinx là hàm số tuần hoàn với chu kỳ 2π. Điều này có nghĩa là đồ thị của hàm số lặp lại sau mỗi khoảng 2π.
- Tính đối xứng: Hàm số y = sinx là hàm số lẻ, tức là sin(-x) = -sinx. Đồ thị của hàm số đối xứng qua gốc tọa độ.
- Các điểm đặc biệt:
- sinx = 0 khi x = kπ, với k là số nguyên (…, -2π, -π, 0, π, 2π, …).
- sinx = 1 khi x = π/2 + k2π, với k là số nguyên (…, -3π/2, π/2, 5π/2, …).
- sinx = -1 khi x = -π/2 + k2π, với k là số nguyên (…, -5π/2, -π/2, 3π/2, …).
Cách Vẽ Đồ Thị Hàm Số y = sinx
Để vẽ đồ thị hàm số y = sinx, ta có thể thực hiện theo các bước sau:
- Xác định các điểm đặc biệt: Tìm các điểm mà sinx = 0, sinx = 1 và sinx = -1. Các điểm này sẽ giúp xác định hình dạng cơ bản của đồ thị.
- Vẽ một chu kỳ cơ bản: Vẽ đồ thị trên một khoảng có độ dài 2π, ví dụ từ 0 đến 2π.
- Lặp lại chu kỳ: Do tính tuần hoàn, ta có thể lặp lại chu kỳ đã vẽ để mở rộng đồ thị ra toàn bộ tập xác định.
- Sử dụng tính đối xứng: Sử dụng tính đối xứng của hàm số để kiểm tra và hoàn thiện đồ thị.
Đồ Thị Hàm Số y = |sinx|
Hàm số y = |sinx| là một biến thể của hàm số y = sinx, trong đó giá trị của hàm luôn không âm. Để vẽ đồ thị hàm số này, ta có thể thực hiện các bước sau:
- Vẽ đồ thị y = sinx: Vẽ đồ thị của hàm số y = sinx như bình thường.
- Lấy đối xứng phần âm: Lấy đối xứng phần đồ thị nằm phía dưới trục hoành qua trục hoành. Phần này sẽ trở thành phần dương, đảm bảo giá trị của hàm số luôn không âm.
- Xóa phần âm (nếu cần): Nếu cần thiết, xóa phần đồ thị ban đầu nằm phía dưới trục hoành để có đồ thị cuối cùng của y = |sinx|.
Đồ thị hàm số y = |sinx| (nét liền) được tạo ra bằng cách giữ nguyên phần đồ thị y = sinx nằm trên trục hoành và lấy đối xứng phần dưới trục hoành qua trục hoành.
Ứng Dụng của Đồ Thị Hàm Số y = sinx
Đồ thị hàm số y = sinx có nhiều ứng dụng trong thực tế, bao gồm:
- Vật lý: Mô tả các dao động điều hòa, sóng âm, sóng điện từ.
- Kỹ thuật: Thiết kế mạch điện, xử lý tín hiệu.
- Toán học: Giải các phương trình lượng giác, nghiên cứu các hàm số tuần hoàn.
- Âm nhạc: Tổng hợp âm thanh, tạo hiệu ứng âm nhạc.
Hiểu rõ về đồ thị hàm số y = sinx là rất quan trọng trong việc nắm vững kiến thức toán học và ứng dụng nó vào thực tiễn. Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và chi tiết về chủ đề này.