Đồ Thị Hàm Mũ: Lý Thuyết, Cách Vẽ và Bài Tập (Có Giải Chi Tiết)

Hàm mũ và đồ thị của nó là một chủ đề quan trọng trong chương trình Toán lớp 12. Bài viết này sẽ cung cấp một cái nhìn toàn diện về đồ Thị Hàm Mũ, bao gồm lý thuyết cơ bản, cách vẽ đồ thị và các bài tập ví dụ minh họa có lời giải chi tiết.

1. Lý Thuyết Về Hàm Số Mũ

1.1. Định Nghĩa và Tính Chất

Hàm số mũ có dạng $y = a^x$, trong đó $a$ là một số thực dương khác 1.

Tập xác định: $D = mathbb{R}$
Tập giá trị: $T = (0; +infty)$

Tính chất:

Nếu $a > 1$: Hàm số đồng biến trên $mathbb{R}$.
Nếu $0 < a < 1$: Hàm số nghịch biến trên $mathbb{R}$.

1.2. Đạo Hàm của Hàm Số Mũ

$(a^x)’ = a^x ln a$
$(e^x)’ = e^x$

2. Đồ Thị Hàm Số Mũ

2.1. Dạng Đồ Thị

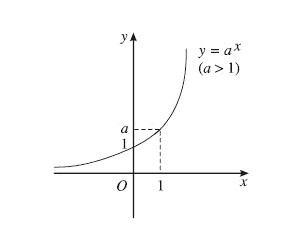
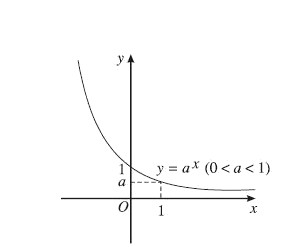
Đồ thị hàm mũ luôn đi qua điểm $(0; 1)$ và nằm phía trên trục hoành. Dạng đồ thị phụ thuộc vào giá trị của cơ số $a$:

Trường hợp $a > 1$: Đồ thị đi lên từ trái sang phải, tiến gần trục hoành khi $x to -infty$.

Trường hợp $0 < a < 1$: Đồ thị đi xuống từ trái sang phải, tiến gần trục hoành khi $x to +infty$.

2.2. Các Bước Vẽ Đồ Thị Hàm Số Mũ

Tìm tập xác định: Xác định tập xác định của hàm số.
Khảo sát sự biến thiên:
- Tính đạo hàm $y’$.
- Tìm khoảng đồng biến, nghịch biến.
- Tìm giới hạn tại vô cực và các tiệm cận (nếu có).
Lập bảng biến thiên.
Vẽ đồ thị:
- Xác định các điểm đặc biệt (giao điểm với trục tung, trục hoành, điểm uốn,…).
- Vẽ đường cong dựa trên bảng biến thiên và các điểm đặc biệt.

2.3. Ví Dụ Minh Họa

Ví dụ: Vẽ đồ thị hàm số $y = 2^x$.

Tập xác định: $D = mathbb{R}$.
Sự biến thiên:
- $y’ = 2^x ln 2 > 0$ với mọi $x in mathbb{R}$. Hàm số đồng biến trên $mathbb{R}$.
- $lim{x to -infty} 2^x = 0$, $lim{x to +infty} 2^x = +infty$.
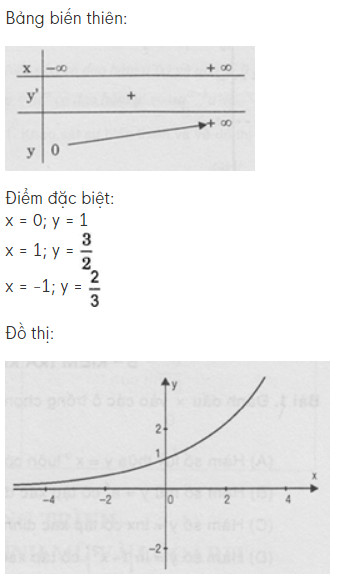
Bảng biến thiên:

$x$ $-infty$ $+infty$

$y’$ +

$y$ 0 $nearrow$ $+infty$
Đồ thị: Đồ thị đi qua điểm $(0; 1)$ và đồng biến trên $mathbb{R}$.

$x$	$-infty$		$+infty$
$y’$		+
$y$	0	$nearrow$	$+infty$

3. Bài Tập Về Đồ Thị Hàm Mũ

Để củng cố kiến thức, các em hãy làm các bài tập sau:

Vẽ đồ thị hàm số $y = (1/3)^x$.
Tìm khoảng đồng biến, nghịch biến của hàm số $y = e^{-x}$.
Xác định hàm số mũ dựa vào đồ thị cho trước.

Hi vọng bài viết này đã cung cấp cho các em đầy đủ kiến thức về đồ thị hàm mũ. Chúc các em học tốt!