Trước khi đi sâu vào khám phá thế giới đồ Thị Hàm Log, chúng ta cùng nhau ôn lại những kiến thức nền tảng về hàm số logarit, một công cụ toán học vô cùng mạnh mẽ và hữu ích. Việc nắm vững lý thuyết là chìa khóa để chinh phục mọi bài tập liên quan đến đồ thị một cách chính xác và nhanh chóng.
Đồ thị hàm số mũ và logarit thể hiện mối quan hệ nghịch đảo giữa hai hàm số, giúp chúng ta hiểu rõ hơn về sự biến thiên của chúng.
1. Tổng Quan Lý Thuyết Về Hàm Số Logarit
1.1. Định Nghĩa Hàm Số Logarit
Hàm số logarit được định nghĩa như sau: Cho số thực $a > 0$ và $a neq 1$, hàm số $y = log_a x$ được gọi là hàm số logarit cơ số $a$.
- Tập xác định: $D = (0; +infty)$.
- Tập giá trị: $T = mathbb{R}$.
1.2. Đạo Hàm Của Hàm Số Logarit
Để vẽ đồ thị hàm log một cách chính xác, việc nắm vững công thức đạo hàm là vô cùng quan trọng. Dưới đây là công thức đạo hàm cơ bản và mở rộng:
- Hàm số $y = log_a x$: $y’ = frac{1}{x ln a}$
- Hàm số $y = log_a u(x)$: $y’ = frac{u'(x)}{u(x) ln a}$
Bảng công thức đạo hàm logarit giúp bạn dễ dàng tra cứu và áp dụng vào bài tập cụ thể.
1.3. Tính Chất Của Hàm Số Logarit
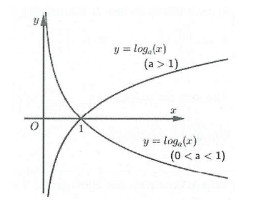
Tính chất của hàm số logarit giúp chúng ta hiểu rõ hơn về sự biến thiên và hình dạng của đồ thị hàm log.
- Tính đơn điệu:
- Nếu $a > 1$: Hàm số đồng biến trên $(0; +infty)$.
- Nếu $0 < a < 1$: Hàm số nghịch biến trên $(0; +infty)$.
- Tiệm cận: Đồ thị hàm số nhận trục tung (x = 0) làm tiệm cận đứng.
- Điểm đặc biệt: Đồ thị luôn đi qua điểm (1; 0).
2. Các Bước Vẽ Đồ Thị Hàm Log
Để vẽ đồ thị hàm log một cách chính xác, bạn có thể thực hiện theo các bước sau:
Bước 1: Tìm tập xác định
Xác định tập xác định của hàm số $y = log_a x$ là $D = (0; +infty)$.
Bước 2: Xét tính đơn điệu
- Nếu $a > 1$, hàm số đồng biến.
- Nếu $0 < a < 1$, hàm số nghịch biến.
Bước 3: Xác định điểm đặc biệt
Đồ thị luôn đi qua điểm (1; 0).
Bước 4: Vẽ đồ thị
Dựa vào tính đơn điệu và điểm đặc biệt, vẽ đồ thị hàm log trên mặt phẳng tọa độ.
Hình ảnh minh họa rõ ràng về hình dạng đồ thị hàm logarit, giúp bạn dễ dàng hình dung và vẽ chính xác.
3. Bài Tập Vận Dụng Đồ Thị Hàm Log
Để củng cố kiến thức và rèn luyện kỹ năng vẽ đồ thị hàm log, hãy cùng xem xét một số ví dụ sau:
Ví dụ 1: Khảo sát và vẽ đồ thị hàm số $y = log_5 x$.
Giải:
-
Tập xác định: $D = (0; +infty)$.
-
Vì $a = 5 > 1$, hàm số đồng biến trên $(0; +infty)$.
-
Đồ thị đi qua điểm (1; 0) và nhận trục tung làm tiệm cận đứng.
-
Bảng biến thiên:
x 0 1 +∞ y’ + y -∞ 0 +∞ 
-
Đồ thị: (Bạn tự vẽ dựa trên các thông tin trên)
Ví dụ 2: Tìm tập xác định của hàm số $y = log_2 (x – 1)$.
Giải:
Để hàm số xác định, ta cần $x – 1 > 0 Rightarrow x > 1$. Vậy tập xác định là $D = (1; +infty)$.
Ví dụ 3: Giải bất phương trình $log_3 (x + 2) < 1$.
Giải:
Điều kiện: $x + 2 > 0 Rightarrow x > -2$.
Bất phương trình tương đương: $x + 2 < 3^1 Rightarrow x < 1$.
Kết hợp điều kiện, ta có: $-2 < x < 1$.
4. Ứng Dụng Của Đồ Thị Hàm Log Trong Thực Tế
Đồ thị hàm log không chỉ là một khái niệm trừu tượng trong toán học, mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau:
- Tài chính: Tính lãi suất kép, phân tích tăng trưởng đầu tư.
- Vật lý: Mô tả sự suy giảm phóng xạ, tính độ lớn của động đất (thang Richter).
- Hóa học: Tính pH của dung dịch.
- Âm nhạc: Mô tả thang âm, cường độ âm thanh (decibel).
Việc hiểu rõ và ứng dụng thành thạo đồ thị hàm log sẽ giúp bạn giải quyết nhiều vấn đề thực tế một cách hiệu quả.
