Hàm số bậc hai và đồ thị của nó, hay còn gọi là parabol, là một khái niệm quan trọng trong toán học, đặc biệt là giải tích. Bài viết này sẽ cung cấp một cái nhìn sâu sắc về đồ Thị Bậc 2, bao gồm định nghĩa, các yếu tố cấu thành, cách vẽ đồ thị, và một số ví dụ minh họa.
1. Định Nghĩa Hàm Số Bậc Hai
Hàm số bậc hai là hàm số được biểu diễn dưới dạng:
(y = a{x^2} + bx + c)
Trong đó:
- (x) là biến số độc lập.
- (a, b, c) là các hằng số thực và (a ne 0). Điều kiện (a ne 0) là bắt buộc để đảm bảo đây là hàm số bậc hai.
Tập xác định của hàm số bậc hai là tập hợp tất cả các số thực (mathbb{R}). Điều này có nghĩa là bạn có thể thay bất kỳ giá trị nào của (x) vào hàm số và sẽ luôn nhận được một giá trị (y) tương ứng.
2. Đồ Thị Hàm Số Bậc Hai: Parabol
Đồ thị của hàm số bậc hai (y = a{x^2} + bx + c) là một đường cong đặc biệt gọi là parabol. Parabol có những đặc điểm sau:
-
Đỉnh: Là điểm cao nhất hoặc thấp nhất của parabol, ký hiệu là (I). Tọa độ đỉnh được tính bằng công thức:
(Ileft( { – frac{b}{{2a}}; – frac{{{b^2} – 4ac}}{{4a}}} right))
Hoặc có thể viết (I(x_I; y_I)) với (x_I = -frac{b}{{2a}}) và (y_I) là giá trị của hàm số tại (x_I), tức (y_I = a{x_I}^2 + bx_I + c).
-
Trục đối xứng: Là đường thẳng đi qua đỉnh và song song với trục tung. Phương trình của trục đối xứng là:
(x = – frac{b}{{2a}})
-
Hướng bề lõm: Parabol có thể quay bề lõm lên trên hoặc xuống dưới, phụ thuộc vào dấu của hệ số (a):
- Nếu (a > 0): Parabol quay bề lõm lên trên (dạng chữ U). Đỉnh là điểm thấp nhất của đồ thị.
- Nếu (a < 0): Parabol quay bề lõm xuống dưới (dạng chữ U ngược). Đỉnh là điểm cao nhất của đồ thị.
3. Các Bước Vẽ Đồ Thị Hàm Số Bậc Hai
Để vẽ đồ thị hàm số (y = a{x^2} + bx + c), bạn có thể thực hiện theo các bước sau:
- Xác định các hệ số a, b, c: Từ phương trình hàm số, xác định giá trị của các hệ số (a, b, c). Điều này giúp bạn xác định hình dạng và hướng của parabol.
- Tìm tọa độ đỉnh I: Sử dụng công thức (Ileft( { – frac{b}{{2a}}; – frac{{{b^2} – 4ac}}{{4a}}} right)) hoặc (x_I = -frac{b}{{2a}}) và (y_I = a{x_I}^2 + bx_I + c) để tìm tọa độ đỉnh của parabol. Đỉnh là điểm quan trọng nhất để vẽ đồ thị.
- Xác định trục đối xứng: Viết phương trình của trục đối xứng là (x = – frac{b}{{2a}}}. Trục đối xứng giúp bạn vẽ parabol một cách cân đối.
- Tìm giao điểm với trục tung: Thay (x = 0) vào phương trình hàm số để tìm giao điểm với trục tung. Điểm này có tọa độ là ((0; c)).
- Tìm giao điểm với trục hoành (nếu có): Giải phương trình (a{x^2} + bx + c = 0) để tìm giao điểm với trục hoành. Số lượng giao điểm phụ thuộc vào giá trị của biệt thức (Delta = b^2 – 4ac):
- Nếu (Delta > 0): Parabol cắt trục hoành tại hai điểm phân biệt.
- Nếu (Delta = 0): Parabol tiếp xúc với trục hoành tại một điểm duy nhất (đỉnh nằm trên trục hoành).
- Nếu (Delta < 0): Parabol không cắt trục hoành.
- Chọn thêm một vài điểm đặc biệt: Chọn một vài giá trị (x) khác nhau (ưu tiên các giá trị gần với trục đối xứng) và tính giá trị (y) tương ứng. Các điểm này sẽ giúp bạn vẽ parabol chính xác hơn. Chú ý rằng, do tính đối xứng, mỗi điểm bạn chọn sẽ có một điểm đối xứng tương ứng qua trục đối xứng.
- Vẽ parabol: Vẽ một đường cong trơn tru đi qua các điểm đã xác định, đảm bảo parabol có hình dạng chữ U (hoặc chữ U ngược) và đối xứng qua trục đối xứng.
4. Ví dụ Minh Họa
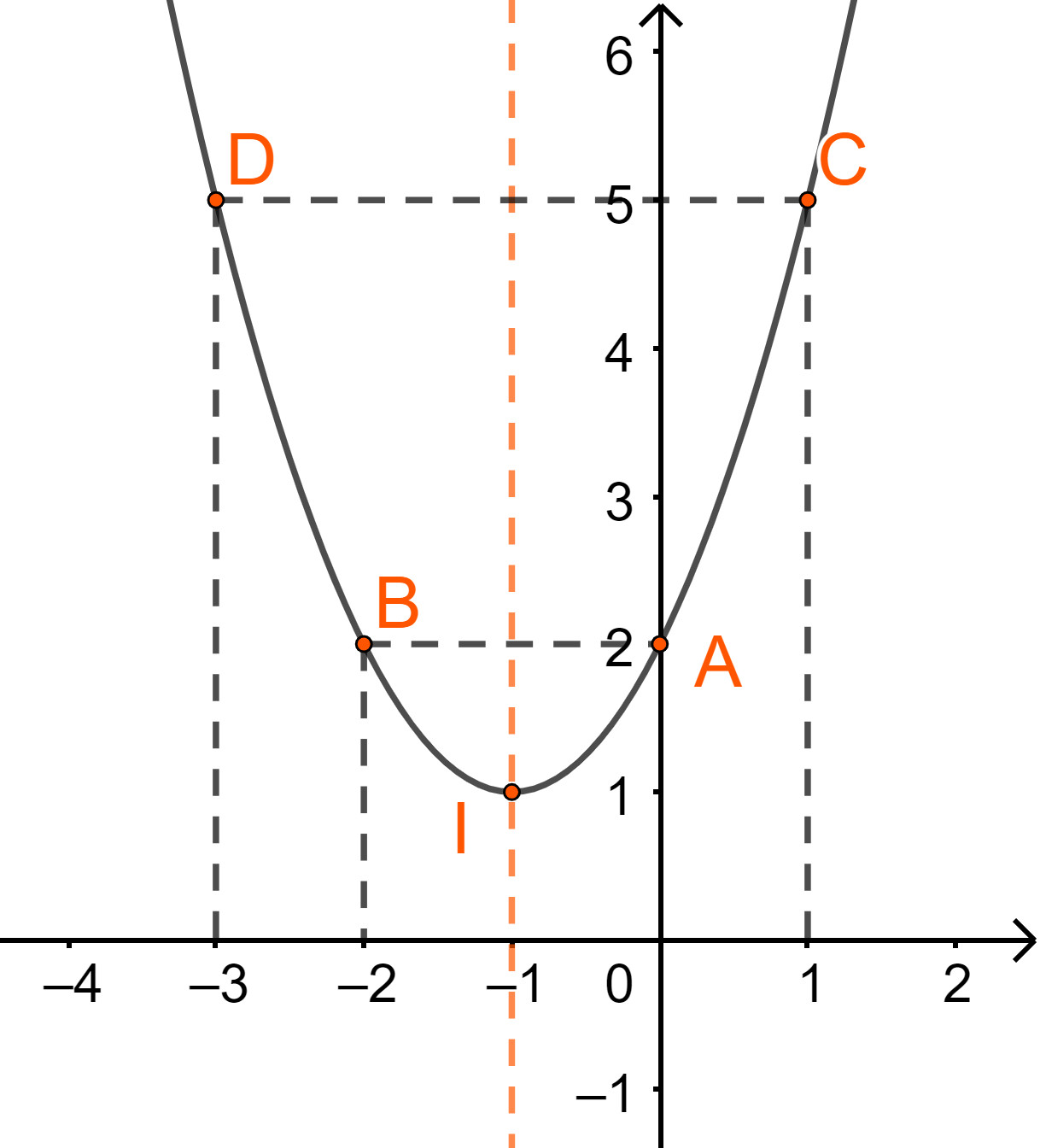
Ví dụ 1: Vẽ đồ thị hàm số (y = {x^2} + 2x + 2)
Hàm số (y = {x^2} + 2x + 2) có (a = 1,b = 2,c = 2)
( Rightarrow – frac{b}{{2a}} = – frac{2}{{2.1}} = – 1;y( – 1) = {( – 1)^2} + 2.( – 1) + 2 = 1)
+ Tọa độ đỉnh (I( – 1;1))
+ Trục đối xứng (x = – 1)
+ Giao điểm với trục tung là A(0;2), không cắt trục hoành (vì (y = {x^2} + 2x + 2 = {(x + 1)^2} + 1 > 0;forall x in mathbb{R}))
+ Lấy điểm B(-2;2) đối xứng với A(0;2) qua trục đối xứng. Điểm C(1;5), D(-3;5) thuộc đồ thị.
Ví dụ 2: Vẽ đồ thị hàm số (y = – {x^2} + 2x)
Hàm số (y = – {x^2} + 2x) có (a = – 1,b = 2,c = 0)
( Rightarrow – frac{b}{{2a}} = – frac{2}{{2.( – 1)}} = 1;y(1) = – {1^2} + 2.1 = 1)
+ Tọa độ đỉnh (I(1;1))
+ Trục đối xứng (x = 1)
+ Giao điểm với trục tung là O(0;0), điểm giao với trục hoành là A(2;0)
+ Lấy điểm B(-1;-3) thuộc đồ thị. Điểm C(3;-3) đối xứng với B(-1;-3) qua trục đối xứng
5. Ứng Dụng Của Đồ Thị Bậc 2
Đồ thị bậc 2 có rất nhiều ứng dụng trong thực tế, bao gồm:
- Vật lý: Mô tả quỹ đạo của vật ném xiên, chuyển động của vật dưới tác dụng của trọng lực.
- Kinh tế: Mô hình hóa chi phí, doanh thu, lợi nhuận. Tìm điểm cực đại, cực tiểu để tối ưu hóa.
- Kỹ thuật: Thiết kế các cấu trúc như cầu, mái vòm, anten parabol.
- Toán học: Giải các bài toán liên quan đến cực trị, tìm giá trị lớn nhất, nhỏ nhất.
Kết luận
Đồ thị bậc 2 là một công cụ mạnh mẽ để mô tả và giải quyết nhiều vấn đề trong toán học và các lĩnh vực khác. Hiểu rõ về định nghĩa, đặc điểm và cách vẽ đồ thị bậc 2 sẽ giúp bạn áp dụng nó một cách hiệu quả trong học tập và công việc.