Độ phân tán là một khái niệm quan trọng trong thống kê, giúp ta đánh giá mức độ trải rộng của dữ liệu. Các số đặc trưng đo độ Phân Tán cho biết các giá trị trong một tập dữ liệu phân bố gần nhau hay xa nhau. Bài viết này sẽ đi sâu vào các phương pháp đo độ phân tán phổ biến, bao gồm khoảng biến thiên, khoảng tứ phân vị, phương sai và độ lệch chuẩn.
1. Khoảng Biến Thiên và Khoảng Tứ Phân Vị
a. Khoảng Biến Thiên
Khoảng biến thiên, còn gọi là biên độ, được tính bằng hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất trong tập dữ liệu.
-
Công thức: Khoảng biến thiên = Giá trị lớn nhất – Giá trị nhỏ nhất.
-
Ý nghĩa: Khoảng biến thiên cho biết phạm vi mà dữ liệu trải rộng. Khoảng biến thiên càng lớn, độ phân tán của dữ liệu càng cao.
-
Ưu điểm: Dễ tính toán và dễ hiểu.
-
Nhược điểm: Chỉ dựa trên hai giá trị cực trị, bỏ qua thông tin từ các giá trị còn lại, và dễ bị ảnh hưởng bởi các giá trị ngoại lệ (outliers).
b. Khoảng Tứ Phân Vị
Khoảng tứ phân vị (IQR) là hiệu giữa tứ phân vị thứ ba (Q3) và tứ phân vị thứ nhất (Q1).
-
Công thức: ΔQ = Q3 – Q1
-
Ý nghĩa: Khoảng tứ phân vị đo độ phân tán của 50% dữ liệu nằm ở giữa. IQR càng lớn, dữ liệu càng phân tán.
-
Ưu điểm: Ít bị ảnh hưởng bởi các giá trị ngoại lệ so với khoảng biến thiên.
-
Nhược điểm: Chỉ sử dụng thông tin của 50% dữ liệu trung tâm, bỏ qua thông tin từ các giá trị ở hai đầu.
2. Phương Sai và Độ Lệch Chuẩn
Phương sai và độ lệch chuẩn là hai thước đo độ phân tán phổ biến, sử dụng tất cả các giá trị trong tập dữ liệu.
Cho mẫu số liệu x1, x2, x3, …, xn, với số trung bình là x̄
-
Độ lệch: của mỗi giá trị xi là (xi – x̄)
-
Phương sai (s²): Là trung bình của bình phương các độ lệch.
- Công thức: s² = [(x₁ – x̄)² + (x₂ – x̄)² + … + (xn – x̄)²] / n
-
Độ Lệch Chuẩn (s): Là căn bậc hai của phương sai.
- Công thức: s = √s²
-
Ý nghĩa: Phương sai và độ lệch chuẩn càng lớn, dữ liệu càng phân tán. Độ lệch chuẩn thường được sử dụng hơn vì có cùng đơn vị với dữ liệu gốc, giúp dễ dàng diễn giải.
-
Chú ý: Đối với dữ liệu được trình bày dưới dạng bảng tần số, phương sai được tính như sau:
s² = [m₁(x₁ – x̄)² + m₂(x₂ – x̄)² + … + mk(xk – x̄)²] / n
Trong đó, mi là tần số của giá trị xi và n = m₁ + m₂ + … + mk
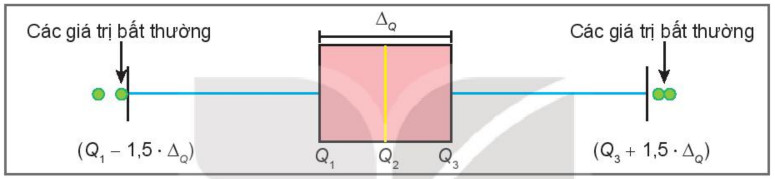
3. Phát Hiện Số Liệu Bất Thường Bằng Biểu Đồ Hộp
Biểu đồ hộp (boxplot) là một công cụ hữu ích để trực quan hóa độ phân tán của dữ liệu và phát hiện các giá trị bất thường (outliers).
-
Giá trị bất thường: Là các giá trị quá lớn hoặc quá nhỏ so với phần lớn các giá trị khác trong tập dữ liệu.
-
Biểu đồ hộp: Thể hiện các tứ phân vị (Q1, Q2, Q3), giá trị lớn nhất, giá trị nhỏ nhất và các giá trị ngoại lệ.
Một giá trị x được xem là bất thường nếu nó nằm ngoài khoảng:
-
x < Q1 – 1.5 IQR hoặc x > Q3 + 1.5 IQR
Kết luận:
Việc hiểu và sử dụng các số đặc trưng đo độ phân tán là rất quan trọng trong phân tích dữ liệu. Tùy thuộc vào mục đích và đặc điểm của dữ liệu, ta có thể lựa chọn phương pháp phù hợp để đánh giá mức độ phân tán và đưa ra những nhận xét chính xác. Khoảng biến thiên đơn giản nhưng dễ bị ảnh hưởng bởi giá trị ngoại lệ, trong khi khoảng tứ phân vị ít bị ảnh hưởng hơn nhưng chỉ sử dụng một phần dữ liệu. Phương sai và độ lệch chuẩn sử dụng toàn bộ dữ liệu, cung cấp thông tin đầy đủ hơn về độ phân tán. Biểu đồ hộp là công cụ trực quan hữu ích để phát hiện các giá trị bất thường.