Độ dài đường chéo là một yếu tố quan trọng trong hình học, đặc biệt khi làm việc với hình vuông và hình chữ nhật. Việc nắm vững cách tính độ Dài đường Chéo không chỉ giúp bạn giải quyết các bài toán hình học một cách dễ dàng mà còn có ứng dụng thực tế trong thiết kế, xây dựng và nhiều lĩnh vực khác.
Đường Chéo Hình Vuông, Hình Chữ Nhật Là Gì?
Đường chéo của hình vuông và hình chữ nhật là đoạn thẳng nối hai đỉnh đối diện của hình. Mỗi hình vuông và hình chữ nhật đều có hai đường chéo và chúng có độ dài bằng nhau.
Cách Tính Độ Dài Đường Chéo Hình Vuông
Tính Chất Của Đường Chéo Hình Vuông
Đường chéo hình vuông có những tính chất đặc biệt, giúp việc tính toán trở nên đơn giản hơn:
- Hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
- Đường chéo chia hình vuông thành hai tam giác vuông cân bằng nhau.
- Giao điểm của hai đường chéo là tâm của đường tròn nội tiếp và ngoại tiếp hình vuông.
Công Thức Tính Độ Dài Đường Chéo Hình Vuông
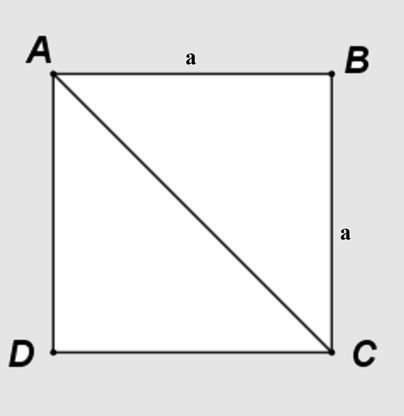
Để tính độ dài đường chéo của hình vuông, ta có thể áp dụng định lý Pytago. Giả sử hình vuông ABCD có cạnh là a, đường chéo AC sẽ chia hình vuông thành hai tam giác vuông cân ABC và ACD.
Áp dụng định lý Pytago cho tam giác vuông ABC:
AC² = AB² + BC² = a² + a² = 2a²
Vậy, độ dài đường chéo AC của hình vuông là:
AC = a√2
Công thức: *Độ dài đường chéo = Cạnh hình vuông √2**
Ví Dụ Minh Họa
Ví dụ 1: Cho một hình vuông có cạnh dài 5cm. Tính độ dài đường chéo của hình vuông này.
Giải:
Áp dụng công thức: Độ dài đường chéo = Cạnh hình vuông * √2
Độ dài đường chéo = 5cm * √2 ≈ 7.07cm
Ví dụ 2: Một hình vuông có độ dài đường chéo là 8cm. Tính độ dài cạnh của hình vuông.
Giải:
Áp dụng công thức: Độ dài đường chéo = Cạnh hình vuông * √2
=> Cạnh hình vuông = Độ dài đường chéo / √2
Cạnh hình vuông = 8cm / √2 ≈ 5.66cm
Cách Tính Độ Dài Đường Chéo Hình Chữ Nhật
Tính Chất Của Đường Chéo Hình Chữ Nhật
Hình chữ nhật là một tứ giác có bốn góc vuông. Đường chéo hình chữ nhật có các tính chất sau:
- Hai đường chéo của hình chữ nhật bằng nhau.
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
- Đường chéo chia hình chữ nhật thành hai tam giác vuông bằng nhau.
Công Thức Tính Độ Dài Đường Chéo Hình Chữ Nhật
Tương tự như hình vuông, ta cũng sử dụng định lý Pytago để tính độ dài đường chéo hình chữ nhật. Giả sử hình chữ nhật ABCD có chiều dài là a và chiều rộng là b. Đường chéo AC sẽ là cạnh huyền của tam giác vuông ABC.
Áp dụng định lý Pytago cho tam giác vuông ABC:
AC² = AB² + BC² = a² + b²
Vậy, độ dài đường chéo AC của hình chữ nhật là:
AC = √(a² + b²)
Công thức: Độ dài đường chéo = √(Chiều dài² + Chiều rộng²)
Ví Dụ Minh Họa
Ví dụ: Một hình chữ nhật có chiều dài 12cm và chiều rộng 7cm. Tính độ dài đường chéo của hình chữ nhật này.
Giải:
Áp dụng công thức: Độ dài đường chéo = √(Chiều dài² + Chiều rộng²)
Độ dài đường chéo = √(12² + 7²) = √(144 + 49) = √193 ≈ 13.89cm
Ứng Dụng Thực Tế Của Việc Tính Độ Dài Đường Chéo
Việc tính toán độ dài đường chéo có nhiều ứng dụng thực tế trong cuộc sống và công việc, bao gồm:
- Xây dựng: Tính toán kích thước và độ vững chắc của các cấu trúc hình chữ nhật và hình vuông.
- Thiết kế: Xác định tỷ lệ và kích thước phù hợp cho các đối tượng thiết kế.
- Nội thất: Tính toán kích thước đồ nội thất để đảm bảo phù hợp với không gian.
- Cắt và đo đạc: Ứng dụng trong việc cắt vật liệu, đo đạc đất đai và các công việc liên quan đến hình học không gian.
Bài Toán Chứng Minh Tứ Giác Là Hình Chữ Nhật Thông Qua Đường Chéo
Tính chất và công thức tính độ dài đường chéo có thể được sử dụng để chứng minh một tứ giác là hình chữ nhật.
Ví dụ: Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, AD. Chứng minh rằng tứ giác EFGH là hình chữ nhật.
Chứng minh:
-
Chứng minh EFGH là hình bình hành:
- EH là đường trung bình của tam giác ABD => EH // BD và EH = 1/2 BD
- FG là đường trung bình của tam giác BCD => FG // BD và FG = 1/2 BD
=> EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
-
Chứng minh EFGH có một góc vuông:
-
EF là đường trung bình của tam giác ABC => EF // AC
-
Vì AC ⊥ BD (gt) mà EH // BD và EF // AC => EH ⊥ EF
-
Hình bình hành EFGH có một góc vuông => EFGH là hình chữ nhật (đpcm)
-
Nắm vững các công thức và tính chất liên quan đến độ dài đường chéo hình vuông và hình chữ nhật sẽ giúp bạn giải quyết nhiều bài toán hình học và ứng dụng chúng một cách hiệu quả trong thực tế.