Độ Dài Đoạn Thẳng AB Trong Mặt Phẳng Oxy
Trong hình học giải tích, việc tính độ Dài đoạn Thẳng Ab là một bài toán cơ bản. Trong mặt phẳng tọa độ Oxy, chúng ta có thể dễ dàng xác định độ dài này thông qua tọa độ của hai điểm A và B.
Tính Độ Dài Vectơ
Trước khi đi vào công thức tính độ dài đoạn thẳng AB, ta cần nắm vững công thức tính độ dài của một vectơ. Cho vectơ $vec{u}=(x,y)$ trong mặt phẳng Oxy, độ dài của vectơ $vec{u}$ được ký hiệu là $|vec{u}|$ và được tính bằng công thức:
$$|vec{u}|=sqrt{x^2+y^2}$$
Công thức này xuất phát từ định lý Pythagoras, xem vectơ như cạnh huyền của một tam giác vuông có các cạnh góc vuông lần lượt là x và y.
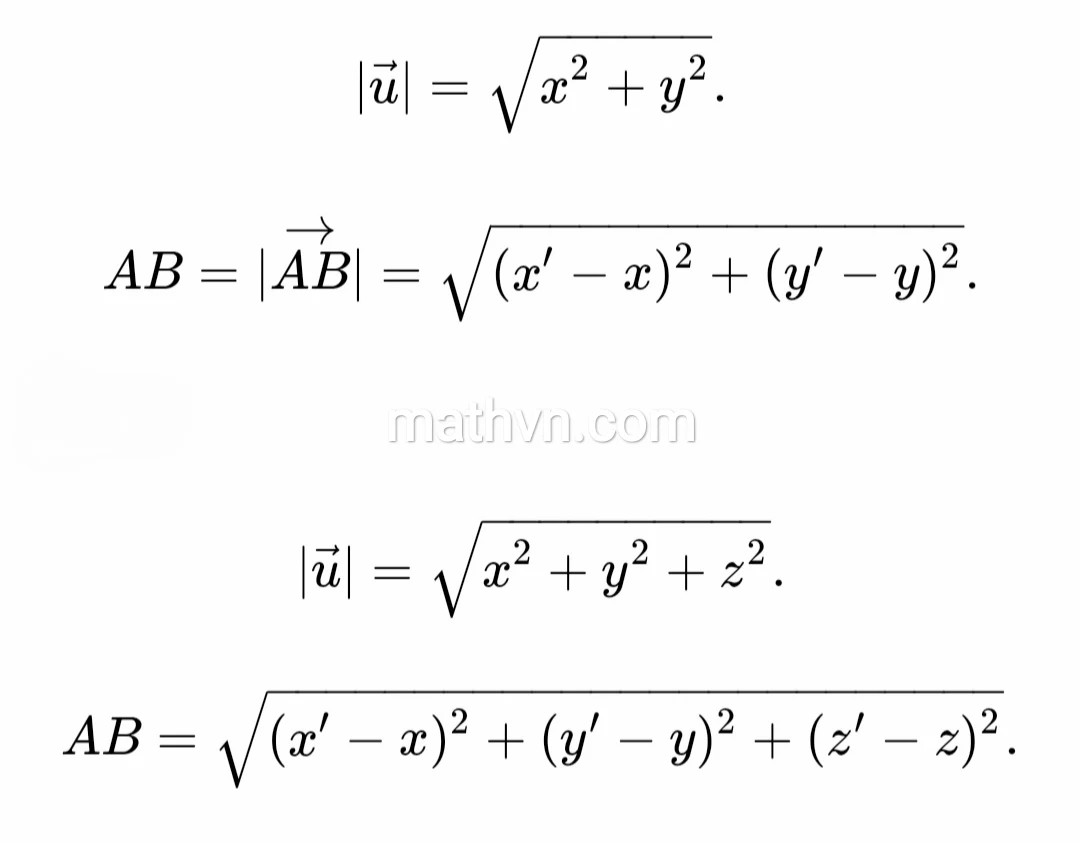Vecto u(x, y) trong mặt phẳng Oxy
Minh họa vectơ u có tọa độ (x, y) trên mặt phẳng Oxy, thể hiện mối liên hệ giữa tọa độ và độ dài vectơ.
Công Thức Tính Độ Dài Đoạn Thẳng AB
Giả sử chúng ta có hai điểm A và B trong mặt phẳng Oxy với tọa độ lần lượt là $A(x_A, y_A)$ và $B(x_B, y_B)$. Độ dài đoạn thẳng AB, ký hiệu là AB hoặc |AB|, chính là độ dài của vectơ $vec{AB}$. Vectơ $vec{AB}$ có tọa độ là $(x_B – x_A, y_B – y_A)$. Do đó, công thức tính độ dài đoạn thẳng AB là:
$$AB = |vec{AB}| = sqrt{(x_B – x_A)^2 + (y_B – y_A)^2}$$
Công thức này cũng dựa trên định lý Pythagoras, trong đó $x_B – x_A$ và $y_B – y_A$ là độ dài các cạnh góc vuông của một tam giác vuông, và AB là độ dài cạnh huyền.
Ví Dụ Minh Họa
Để hiểu rõ hơn về cách áp dụng công thức, xét ví dụ sau:
Cho hai điểm $A(1, 2)$ và $B(4, 6)$ trong mặt phẳng Oxy. Hãy tính độ dài đoạn thẳng AB.
Áp dụng công thức, ta có:
$AB = sqrt{(4 – 1)^2 + (6 – 2)^2} = sqrt{3^2 + 4^2} = sqrt{9 + 16} = sqrt{25} = 5$
Vậy độ dài đoạn thẳng AB là 5 đơn vị.
Độ Dài Đoạn Thẳng AB Trong Không Gian Oxyz
Tương tự như trong mặt phẳng, việc tính độ dài đoạn thẳng AB trong không gian Oxyz cũng dựa trên tọa độ của hai điểm A và B.
Tính Độ Dài Vectơ Trong Không Gian
Cho vectơ $vec{u}=(x,y,z)$ trong không gian Oxyz, độ dài của vectơ $vec{u}$ được tính bằng công thức:
$$|vec{u}|=sqrt{x^2+y^2+z^2}$$
Công thức này là một mở rộng của định lý Pythagoras cho không gian ba chiều.
Công Thức Tính Độ Dài Đoạn Thẳng AB Trong Không Gian
Giả sử chúng ta có hai điểm A và B trong không gian Oxyz với tọa độ lần lượt là $A(x_A, y_A, z_A)$ và $B(x_B, y_B, z_B)$. Độ dài đoạn thẳng AB được tính bằng công thức:
$$AB = sqrt{(x_B – x_A)^2 + (y_B – y_A)^2 + (z_B – z_A)^2}$$
Đây là công thức tổng quát để tính khoảng cách giữa hai điểm trong không gian ba chiều.
Ví Dụ Minh Họa
Xét ví dụ sau:
Cho hai điểm $A(1, 2, 3)$ và $B(4, 6, 8)$ trong không gian Oxyz. Hãy tính độ dài đoạn thẳng AB.
Áp dụng công thức, ta có:
$AB = sqrt{(4 – 1)^2 + (6 – 2)^2 + (8 – 3)^2} = sqrt{3^2 + 4^2 + 5^2} = sqrt{9 + 16 + 25} = sqrt{50} = 5sqrt{2}$
Vậy độ dài đoạn thẳng AB là $5sqrt{2}$ đơn vị.
Việc nắm vững công thức tính độ dài đoạn thẳng AB trong cả mặt phẳng Oxy và không gian Oxyz là rất quan trọng trong hình học giải tích và có nhiều ứng dụng trong các bài toán liên quan đến khoảng cách và vị trí tương đối giữa các điểm.