Hình tứ giác là một trong những hình học cơ bản và quan trọng, xuất hiện thường xuyên trong các bài tập toán học. Việc nắm vững kiến thức về tứ giác giúp học sinh tự tin hơn trong quá trình học tập. Bài viết này sẽ cung cấp đầy đủ và chi tiết về “định Nghĩa Tứ Giác” và các kiến thức liên quan.
Định nghĩa tứ giác
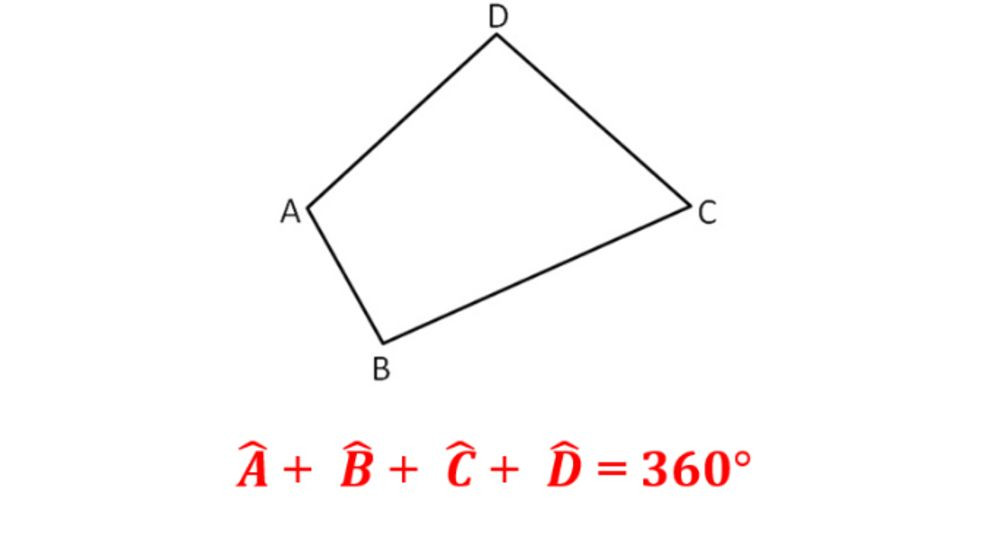
Định nghĩa hình tứ giác:
- Hình tứ giác là một đa giác có 4 đỉnh và 4 cạnh, trong đó không có bất kỳ 2 đoạn thẳng nào cùng nằm trên một đường thẳng.
- Phân loại: Tứ giác có thể là tứ giác kép (có cặp cạnh đối cắt nhau) hoặc tứ giác đơn (lồi hoặc lõm, không có cặp cạnh nào đối nhau).
- Kí hiệu: Hình tứ giác được kí hiệu ABCD, tổng các góc của tứ giác là 360 độ, cụ thể: ∠A + ∠B + ∠C + ∠D = 360°.
Ví dụ hình tứ giác ABCD.
Tính chất của hình tứ giác
Học sinh cần nắm vững hai tính chất quan trọng của hình tứ giác: tính chất đường chéo và tính chất góc.
- Tính chất 1 – Tính chất đường chéo của hình tứ giác: Hai đường chéo của hình tứ giác lồi giao nhau tại một điểm thuộc miền trong của tứ giác. Ngược lại, nếu tứ giác có hai đường chéo giao nhau tại một điểm thuộc miền trong của nó, thì đó là tứ giác lồi.
- Tính chất 2 – Tính chất góc của hình tứ giác: Tổng số đo bốn góc trong của hình tứ giác luôn bằng 360 độ.
Tổng 4 góc của hình tứ giác bằng 360 độ.
Phân loại hình tứ giác và cách nhận biết
Các dạng tứ giác thường gặp được chia thành 4 loại cơ bản. Cách nhận biết từng loại tứ giác như sau:
- Tứ giác đơn: Là các hình tứ giác không có cạnh nào cắt nhau.
- Tứ giác lõm: Là hình tứ giác chứa một góc có số đo lớn hơn 180 độ và một trong hai đường chéo nằm bên ngoài tứ giác.
- Tứ giác lồi: Là tứ giác có 4 góc đều nhỏ hơn 180 độ, 2 đường chéo của tứ giác nằm phía bên trong của hình này. Tức là, tứ giác lồi là hình tứ giác luôn thuộc một nửa mặt phẳng có chứa bất kỳ cạnh nào.
- Tứ giác không đều: Là các hình tứ giác không có cặp cạnh nào song song với nhau và thường được sử dụng để đại diện cho dạng tứ giác lồi.
Hình tứ giác lồi.
Một số dạng hình tứ giác đặc biệt
Ngoài 4 dạng tứ giác cơ bản, trong toán học còn có một số dạng hình tứ giác đặc biệt. Học sinh cần nắm rõ đặc điểm nhận biết các dạng hình tứ giác đặc biệt đó như sau:
1. Hình thang
Hình thang là hình tứ giác có ít nhất hai cạnh đối song song.
Hình thang có ít nhất 2 cạnh đối song song.
2. Hình thang cân
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau. Điều này dẫn đến các tính chất sau:
- Hình tứ giác có ít nhất 2 cạnh đối song song.
- Hình thang có 2 góc kề cùng 1 cạnh đáy bằng nhau.
- Hình thang có 2 đường chéo bằng nhau.
3. Hình bình hành
Hình bình hành là hình tứ giác có hai cặp cạnh đối song song. Các tính chất khác bao gồm: các góc đối bằng nhau, các cạnh đối bằng nhau, hai đường chéo cắt nhau tại trung điểm của mỗi đường. Hình bình hành là trường hợp đặc biệt của hình thang.
Hình bình hành có 2 cặp cạnh đối song song.
4. Hình thoi
Hình thoi là hình tứ giác có bốn cạnh bằng nhau.
Hình thoi là hình tứ giác có 4 cạnh bằng nhau.
5. Hình chữ nhật
Hình chữ nhật là hình tứ giác có bốn góc vuông. Điều này dẫn đến các tính chất: hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Hình chữ nhật là hình tứ giác có 4 góc vuông.
6. Hình vuông
Hình vuông là hình tứ giác có bốn góc vuông và bốn cạnh bằng nhau. Nó kế thừa tất cả các tính chất của hình chữ nhật và hình thoi.
Hình vuông có 4 góc vuông, 4 cạnh bằng nhau.
7. Tứ giác nội tiếp
Tứ giác nội tiếp là tứ giác có bốn đỉnh nằm trên cùng một đường tròn. Đường tròn này được gọi là đường tròn ngoại tiếp tứ giác.
Tứ giác nội tiếp có 4 đỉnh nằm trên cùng 1 đường tròn.
Các công thức hình tứ giác
Khi học về hình tứ giác, không thể bỏ qua các công thức tính chu vi và diện tích.
Công thức chu vi tứ giác
Chu vi của tứ giác được tính bằng tổng độ dài của bốn cạnh.
P = a + b + c + d
Trong đó:
- P: là chu vi hình tứ giác
- a, b, c, d: chiều dài 4 cạnh của tứ giác
Ví dụ: Cho hình tứ giác ABCD có chiều dài các cạnh AB = a = 5cm, BC = b = 7cm, CD = c = 9cm, DA = d = 5cm. Tính chu vi hình tứ giác ABCD.
Lời giải: Chu vi hình tứ giác ABCD là:
P = a + b + c + d = 5 + 7 + 9 + 5 = 26cm
Vậy chu vi hình tứ giác ABCD là 26cm.
Công thức diện tích tứ giác
Công thức tính diện tích tứ giác phụ thuộc vào dạng hình tứ giác đó và không có công thức chung. Ví dụ:
- Công thức tính diện tích hình vuông: S = a x a (Trong đó S là diện tích hình vuông, a là chiều dài cạnh hình vuông)
- Công thức tính diện tích hình chữ nhật: S = a x b (Trong đó S là diện tích hình chữ nhật, a là chiều dài hình chữ nhật, b là chiều rộng hình chữ nhật)
- Công thức tính diện tích hình bình hành: S = a x h (Trong đó S là diện tích hình bình hành, a là chiều dài cạnh đáy hình bình hành, h là chiều cao hạ từ đỉnh xuống cạnh đáy hình bình hành)
…
Luyện tập một số dạng toán về hình tứ giác
Các dạng bài tập dành cho học sinh chủ yếu tập trung vào các kiến thức cơ bản. Do đó, các em nên luyện tập một số dạng bài tập về hình tứ giác như sau:
Dạng 1: Bài tập về định nghĩa và công thức
Các bài tập trắc nghiệm về định nghĩa, công thức, nhận dạng hình tứ giác giúp học sinh ghi nhớ kiến thức.
Ví dụ: Hình tứ giác có 4 góc vuông, 4 cạnh bằng nhau, các cạnh đối song song là hình gì?
- Hình chữ nhật
- Hình thoi
- Hình vuông
- Hình bình hành
Đáp án: 3. Hình vuông
Dạng 2: Nhận biết các dạng hình tứ giác
Yêu cầu trẻ nhận biết các hình tứ giác thông qua hình ảnh hoặc mô tả.
Ví dụ 1: Tìm hình tứ giác luôn nằm trong nửa mặt phẳng có bờ là đường thẳng chứa bất kỳ cạnh nào của tam giác?
Đáp án: Tứ giác lồi.
Ví dụ 2: Tìm các hình tứ giác có trong hình dưới đây:
Đáp án: Các hình tứ giác có trong hình là DEIH, HIFG, DEFG.
Ví dụ 3: Tìm hình thang trong các hình dưới đây?
Đáp án: hình thang là các hình 1, hình 2, hình 4, hình 5, hình 6.
Dạng 3: Tính chu vi, diện tích của hình tứ giác
Với các dữ kiện cho trước, học sinh cần tính toán chu vi hoặc diện tích theo yêu cầu của đề bài.
Ví dụ 1: Cho hình tứ giác EFMN, biết tổng số đo các cạnh EF và FM là 52cm, tổng số đo các cạnh MN và NE là 21cm. Tính chu vi hình tứ giác EFMN.
Đáp án: Áp dụng công thức P = a + b + c + d, ta có chu vi hình tứ giác EFMN là:
P = EF + FM + MN + NE = 52 + 21 = 73cm.
Chu vi hình tứ giác EFMN là 73cm.
Ví dụ 2: Cho hình chữ nhật có chiều dài là 8cm, chu vi là 28cm. Tính chiều rộng của hình chữ nhật?
Đáp án: Áp dụng công thức tính chu vi hình chữ nhật là P = (a + b) x 2
=> Tổng 2 cạnh là chiều dài và chiều rộng hình chữ nhật là: a + b = P/2 = 28/2 = 14cm
=> Chiều rộng hình chữ nhật là: 14 – 8 = 6cm
Vậy chiều rộng hình chữ nhật là 6cm.
Ví dụ 3: Tính diện tích hình vuông, biết chiều dài cạnh góc vuông là 5cm.
Đáp án: Áp dụng công thức tính diện tích hình vuông là S = a x a
=> Diện tích hình vuông là: 5 x 5 = 25cm²
Vậy diện tích hình vuông có cạnh 5cm là 25cm².
Dạng 4: Tính các góc của hình tứ giác
Áp dụng kiến thức tổng các góc trong của hình tứ giác là 360 độ để tính số đo góc.
Ví dụ: Tính tổng các góc ngoài của hình tứ giác ABCD.
Đáp án: Vận dụng kiến thức 2 góc kề bù có tổng là 180 độ và tổng các góc trong hình tứ giác là 360 độ. Tổng các góc ngoài của hình tứ giác ABCD là 360 độ.
Bí quyết ghi nhớ hiệu quả kiến thức về hình tứ giác
Để giúp trẻ ghi nhớ hiệu quả kiến thức về hình tứ giác, phụ huynh nên áp dụng một số bí quyết sau:
Nắm vững kiến thức cơ bản
Đảm bảo trẻ nắm vững định nghĩa, phân loại, nhận biết các dạng hình tứ giác, các công thức tính diện tích và chu vi.
Học đi đôi với hành
Giải quyết các dạng bài tập liên quan, bắt đầu từ cơ bản đến nâng cao.
Sử dụng phần mềm học toán sinh động
Chọn lựa các phần mềm học toán uy tín để trẻ hứng thú hơn.
Hy vọng bài viết này cung cấp đầy đủ kiến thức về “định nghĩa tứ giác” và các vấn đề liên quan. Chúc các em học tốt!