Định lý Ta-let là một trong những định lý cơ bản và quan trọng nhất trong hình học phẳng, đặc biệt là trong việc nghiên cứu tam giác. Nó không chỉ là một công cụ mạnh mẽ để giải quyết các bài toán hình học mà còn là nền tảng cho nhiều khái niệm và định lý khác phức tạp hơn. Bài viết này sẽ đi sâu vào định lý Ta-let, định lý đảo, hệ quả và các ứng dụng của nó, đồng thời cung cấp các ví dụ minh họa và bài tập để bạn đọc nắm vững kiến thức.
1. Định Lý Ta-Let Thuận
Định lý Ta-let phát biểu rằng: “Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.”
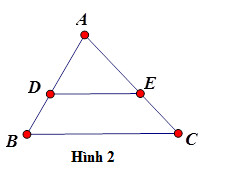
Giả sử ta có tam giác ABC, đường thẳng DE song song với cạnh BC (D thuộc AB, E thuộc AC). Khi đó, theo định lý Ta-let, ta có tỉ lệ thức sau:
$dfrac{AD}{DB} = dfrac{AE}{EC}$
Định lý này là cơ sở để giải quyết nhiều bài toán liên quan đến việc tính toán độ dài các đoạn thẳng trong tam giác.
Hình ảnh minh họa định lý Ta-let thuận trong tam giác ABC, với đường thẳng DE song song BC.
2. Định Lý Ta-Let Đảo
Định lý Ta-let đảo là một công cụ hữu ích để chứng minh hai đường thẳng song song. Nó phát biểu như sau: “Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.”
Nói cách khác, nếu trong tam giác ABC, ta có đường thẳng DE cắt AB tại D và AC tại E sao cho:
$dfrac{AD}{DB} = dfrac{AE}{EC}$
thì ta có thể kết luận rằng DE song song với BC.
Hình ảnh minh họa định lý Ta-let đảo, chứng minh DE song song BC dựa trên tỉ lệ các đoạn thẳng.
Ví dụ: Cho tam giác ABC có AD/DB = AE/EC => DE // BC. Định lý Ta-let đảo giúp ta chứng minh sự song song của hai đường thẳng dựa trên tỷ lệ đoạn thẳng.
3. Hệ Quả Của Định Lý Ta-Let
Hệ quả của định lý Ta-let mở rộng phạm vi ứng dụng của định lý này. Nó phát biểu rằng: “Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.”
Trong tam giác ABC, nếu DE song song với BC (D thuộc AB, E thuộc AC) thì ta có:
$dfrac{AD}{AB} = dfrac{AE}{AC} = dfrac{DE}{BC}$
Hệ quả này cho phép ta so sánh tỉ lệ giữa các cạnh của hai tam giác đồng dạng được tạo ra.
Hình ảnh minh họa hệ quả định lý Ta-let, thể hiện sự đồng dạng và tỉ lệ giữa tam giác ADE và ABC.
Chú ý: Hệ quả trên vẫn đúng cho trường hợp đường thẳng a song song với một cạnh của tam giác và cắt phần kéo dài của hai cạnh còn lại.
Hình ảnh minh họa trường hợp mở rộng của hệ quả định lý Ta-let khi đường thẳng song song cắt phần kéo dài của cạnh.
Ở hai hình trên ΔABC có BC // B’C’ => AB’/AB = AC’/AC = B’C’/BC. Trường hợp này mở rộng phạm vi áp dụng của định lý.
4. Các Dạng Toán Thường Gặp Về Định Lý Ta-Let
Định lý Ta-let được ứng dụng rộng rãi trong nhiều dạng bài toán khác nhau. Dưới đây là một số dạng toán thường gặp:
Dạng 1: Tính Độ Dài Đoạn Thẳng, Chu Vi, Diện Tích và Các Tỉ Số
Phương pháp giải: Sử dụng trực tiếp định lý Ta-let, hệ quả của định lý Ta-let và các tính chất của tỉ lệ thức để thiết lập mối quan hệ giữa các đoạn thẳng và tính toán.
Ví dụ: Cho tam giác ABC, DE // BC (D thuộc AB, E thuộc AC). Biết AD = 4cm, DB = 6cm, AE = 5cm. Tính EC.
Giải: Theo định lý Ta-let, ta có:
$dfrac{AD}{DB} = dfrac{AE}{EC} Rightarrow dfrac{4}{6} = dfrac{5}{EC} Rightarrow EC = dfrac{5 cdot 6}{4} = 7.5 ,cm$
Dạng 2: Chứng Minh Hai Đường Thẳng Song Song, Chứng Minh Các Đẳng Thức Hình Học
Phương pháp giải: Sử dụng định lý Ta-let đảo và hệ quả của định lý Ta-let để chứng minh.
Ví dụ: Cho tam giác ABC, trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD/AB = AE/AC. Chứng minh rằng DE // BC.
Giải: Theo giả thiết, ta có AD/AB = AE/AC. Áp dụng định lý Ta-let đảo, ta kết luận được DE // BC.
5. Bài Tập Vận Dụng Định Lý Ta-Let
Để củng cố kiến thức, chúng ta sẽ cùng nhau giải một số bài tập vận dụng định lý Ta-let.
Bài 1. Cho hình vẽ với AB
Hãy chọn câu sai.
A. (dfrac{{AD}}{{AB}} = dfrac{{AE}}{{AC}} Rightarrow DE//BC).
B. (dfrac{{AD}}{{DB}} = dfrac{{AE}}{{EC}} Rightarrow DE//BC).
C. (dfrac{{AB}}{{DB}} = dfrac{{AC}}{{EC}} Rightarrow DE//BC).
D. (dfrac{{AD}}{{DE}} = dfrac{{AE}}{{ED}} Rightarrow DE//BC).
Lời giải: Theo định lý đảo của định lý Ta-lét: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Nên D sai.
Chọn đáp án D.
Bài 2. Cho hình vẽ, trong đó $DE{rm{//}}BC$, $AD = 12,,,DB = 18,,,CE = 30$. Độ dài $AC$ bằng:
A. (20)
B. (dfrac{{18}}{{25}})
C. (50)
D. (45)
Lời giải: Vì $DE{rm{//}}BC$, theo định lý Ta-lét ta có (dfrac{{AD}}{{BD}} = dfrac{{AE}}{{EC}} Leftrightarrow dfrac{{12}}{{18}} = dfrac{{AE}}{{30}})( Rightarrow EA = dfrac{{30.12}}{{18}} = 20,cm)
Nên (AC = AE + EC = 50,cm)
Chọn đáp án C.
Bài 3. Tính các độ dài $x,y$ trong hình bên:
A. (x = 2sqrt 5 ,;y = 10)
B. (x = 10sqrt 5 ,;y = 9)
C. (x = 6sqrt 5 ,;y = 10)
D. (x = 5sqrt 5 ,;y = 10)()
Lời giải: Áp dụng định lý Py-ta-go cho tam giác vuông (OA’B’), ta có:
(begin{array}{l}OA{‘^2} + A’B{‘^2} = OB{‘^2}\ Leftrightarrow {2^2} + {4^2} = OB{‘^2}\ Leftrightarrow OB{‘^2} = 20\ Rightarrow OB’ = sqrt {20} end{array})
(A’B’ bot AA’,;AB bot AA’ Rightarrow A’B’parallel AB) (Theo định lý từ vuông góc đến song song)
Áp dụng định lý Ta-let, ta có:
(dfrac{{OA’}}{{OA}} = dfrac{{OB’}}{{OB}} = dfrac{{A’B’}}{{AB}})
( Rightarrow left{ begin{array}{l}dfrac{{sqrt {20} }}{x} = dfrac{2}{5}\dfrac{4}{y} = dfrac{2}{5}end{array} right. Leftrightarrow left{ begin{array}{l}x = dfrac{{5.sqrt {20} }}{2} = 5sqrt 5 \y = dfrac{{4.5}}{2} = 10end{array} right.)
Vậy (x = 5sqrt 5 ) và (y = 10).
Chọn đáp án D.
Bài 4. Cho hình vẽ sau. Có bao nhiêu cặp đường thẳng song song?
A. 0
B. 1
C. 2
D. 3
Lời giải: Ta có: (frac{{MN}}{{PQ}} = frac{4}{8} = frac{1}{2};frac{{ON}}{{OP}} = frac{{3,5}}{{3 + 4}} = frac{1}{2} Rightarrow frac{{MN}}{{PQ}} = frac{{ON}}{{OP}})
( Leftrightarrow MN // PQ) (định lý Thalès đảo) (1)
Ta có: (frac{{OE}}{{PE}} = frac{3}{4};frac{{OF}}{{FQ}} = frac{{2,4}}{{3,2}} = frac{3}{4} Rightarrow frac{{OE}}{{PE}} = frac{{OF}}{{FQ}})
( Rightarrow EF // PQ) (định lý Thalès đảo) (2)
Từ (1), (2) ( Rightarrow MN // EF) (cùng song song với (PQ) ).
Vậy có 3 cặp đường thẳng song song.
Chọn đáp án D.
Bài 5. Cho tứ giác (ABCD) có (O) là giao điểm của hai đường chéo. Đường thẳng qua (A) và song song với (BC) cắt (BD) ở (E) . Đường thẳng qua (B) song song với (AD) cắt (AC) ở (F) . Chọn kết luận sai?
A. (frac{{OE}}{{OB}} = frac{{OA}}{{OC}})
B. (frac{{EF}}{{AB}} = frac{{OE}}{{OB}})
C. (frac{{OB}}{{OD}} = frac{{OF}}{{OA}})
D. (frac{{OE}}{{OD}} = frac{{OF}}{{OC}})
Lời giải:
Hình ảnh minh họa bài toán liên quan đến tứ giác và các đường thẳng song song.
(AE // BC) nên theo hệ quả của định lí Thalès ta có: (frac{{OE}}{{OB}} = frac{{OA}}{{OC}}) (1)
(BF // AD) nên theo hệ quả của định lí Thalès ta có: (frac{{OB}}{{OD}} = frac{{OF}}{{OA}}) (2) Từ (1), (2) ( Rightarrow frac{{OE}}{{OB}} cdot frac{{OB}}{{OD}} = frac{{OA}}{{OC}} cdot frac{{OF}}{{OA}}) hay (frac{{OE}}{{OD}} = frac{{OF}}{{OC}})
Chọn đáp án B.
6. Ứng Dụng Thực Tế Của Định Lý Ta-Let
Định lý Ta-let không chỉ có ý nghĩa trong học thuật mà còn được ứng dụng trong nhiều lĩnh vực của đời sống, kỹ thuật và xây dựng. Một số ứng dụng tiêu biểu bao gồm:
- Đo chiều cao của vật thể: Sử dụng bóng nắng và định lý Ta-let để tính chiều cao của cây, cột điện, tòa nhà,…
- Chia đoạn thẳng thành các phần bằng nhau: Dựng các đường thẳng song song để chia một đoạn thẳng thành nhiều phần có độ dài bằng nhau.
- Thiết kế kỹ thuật: Ứng dụng trong việc thiết kế các công trình kiến trúc, cơ khí, điện tử,…
Kết Luận
Định lý Ta-let là một công cụ mạnh mẽ và linh hoạt trong hình học. Việc nắm vững định lý này, định lý đảo, hệ quả và các ứng dụng của nó sẽ giúp bạn giải quyết các bài toán hình học một cách hiệu quả và mở ra cánh cửa khám phá những kiến thức hình học phức tạp hơn. Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và sâu sắc về định lý Ta-let. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng thành công vào thực tế.