Trong hình học Euclid, định Lý 2 đường Thẳng Song Song là một khái niệm nền tảng, giúp chúng ta hiểu và giải quyết nhiều bài toán liên quan đến đường thẳng và góc. Bài viết này sẽ đi sâu vào định nghĩa, dấu hiệu nhận biết, tiên đề, tính chất và ứng dụng của hai đường thẳng song song.
1. Định Nghĩa và Khái Niệm Cơ Bản
Hai đường thẳng được gọi là song song nếu chúng không có bất kỳ điểm chung nào trên cùng một mặt phẳng. Điều này có nghĩa là, dù kéo dài đến vô tận, chúng cũng không bao giờ cắt nhau.
Kí hiệu: (a // b) (đọc là “đường thẳng a song song với đường thẳng b”).
Lưu ý: Trong mặt phẳng, hai đường thẳng phân biệt chỉ có thể ở một trong hai trạng thái: cắt nhau tại một điểm hoặc song song.
2. Dấu Hiệu Nhận Biết Hai Đường Thẳng Song Song
Để chứng minh hai đường thẳng song song, chúng ta thường dựa vào các dấu hiệu sau:
-
Dấu hiệu 1: Nếu một đường thẳng cắt hai đường thẳng khác và tạo thành một cặp góc so le trong bằng nhau, thì hai đường thẳng đó song song.
-
Dấu hiệu 2: Nếu một đường thẳng cắt hai đường thẳng khác và tạo thành một cặp góc đồng vị bằng nhau, thì hai đường thẳng đó song song.
-
Dấu hiệu 3: Nếu một đường thẳng cắt hai đường thẳng khác và tạo thành một cặp góc trong cùng phía bù nhau (tổng bằng 180 độ), thì hai đường thẳng đó song song.
Ngoài ra, nếu một đường thẳng cắt hai đường thẳng khác và tạo thành một cặp góc so le ngoài bằng nhau, thì hai đường thẳng đó song song.
3. Tiên Đề Ơ-clit Về Đường Thẳng Song Song
Tiên đề Ơ-clit phát biểu rằng: “Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng duy nhất song song với đường thẳng đó.” Đây là một trong những tiên đề cơ bản nhất của hình học Euclid, khẳng định tính duy nhất của đường thẳng song song.
4. Tính Chất Của Hai Đường Thẳng Song Song
Khi hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba (gọi là đường thẳng cắt ngang), sẽ tạo ra các cặp góc có mối quan hệ đặc biệt:
- Hai góc so le trong bằng nhau.
- Hai góc đồng vị bằng nhau.
- Hai góc trong cùng phía bù nhau (tổng bằng 180 độ).
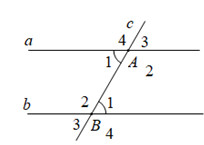
Ví dụ: Nếu (a // b), và đường thẳng c cắt a và b, ta có:
- (widehat{A_1} = widehat{B_1}) (so le trong)
- (widehat{A_3} = widehat{B_1}) (đồng vị)
- (widehat{A_2} + widehat{B_1} = 180^o) (trong cùng phía)
5. Ứng Dụng và Các Dạng Toán Thường Gặp
Định lý 2 đường thẳng song song được ứng dụng rộng rãi trong việc giải các bài toán hình học, đặc biệt là:
- Dạng 1: Chứng minh hai đường thẳng song song: Sử dụng các dấu hiệu nhận biết (góc so le trong bằng nhau, góc đồng vị bằng nhau, góc trong cùng phía bù nhau).
- Dạng 2: Tính số đo góc: Dựa vào tính chất của hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba để tìm ra mối liên hệ giữa các góc và tính toán.
- Dạng 3: Xác định các góc bằng nhau hoặc bù nhau: Sử dụng tính chất của hai đường thẳng song song để suy ra các góc bằng nhau hoặc bù nhau.
Ví dụ minh họa:
Cho hình vẽ, biết (widehat{A_1} = 50^o). Tính (widehat{B_1}) để a // b.
Giải:
Để a // b, ta cần (widehat{A_1} = widehat{B_1}) (hai góc đồng vị).
Vậy, (widehat{B_1} = 50^o).
6. Cách Vẽ Hai Đường Thẳng Song Song
Có nhiều cách để vẽ hai đường thẳng song song, một trong những cách phổ biến nhất là sử dụng thước và êke:
- Vẽ một đường thẳng a.
- Đặt một cạnh của êke trùng với đường thẳng a.
- Đặt thước dọc theo cạnh còn lại của êke.
- Trượt êke dọc theo thước để vẽ đường thẳng b. Đường thẳng b sẽ song song với đường thẳng a.
Kết luận
Định lý 2 đường thẳng song song là một kiến thức quan trọng trong hình học, giúp chúng ta giải quyết nhiều bài toán và hiểu sâu hơn về mối quan hệ giữa các đường thẳng và góc. Việc nắm vững các định nghĩa, dấu hiệu nhận biết, tính chất và ứng dụng của nó sẽ giúp ích rất nhiều trong học tập và cuộc sống.