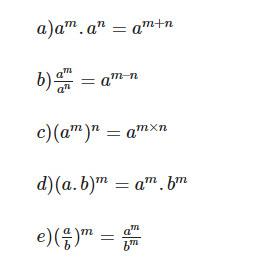Để chinh phục các bài toán về hàm lũy thừa, việc nắm vững điều Kiện Hàm Lũy Thừa là vô cùng quan trọng. Bài viết này sẽ cung cấp cho bạn kiến thức đầy đủ, chi tiết và dễ hiểu nhất về điều kiện xác định của hàm số lũy thừa, cùng với các ví dụ minh họa và bài tập áp dụng để bạn luyện tập.
Hình ảnh minh họa các trường hợp cơ bản của hàm lũy thừa, bao gồm cơ số, số mũ và điều kiện đi kèm.
1. Tổng Quan Về Lũy Thừa và Hàm Số Lũy Thừa
1.1. Lũy Thừa
Lũy thừa là một phép toán số học, ký hiệu là , trong đó a là cơ số và n là số mũ. Khi n là một số nguyên dương, lũy thừa biểu thị phép nhân lặp đi lặp lại của cơ số a n lần.
Để xác định điều kiện hàm lũy thừa chính xác, bạn cần nắm vững các tính chất sau:
Tính chất về đẳng thức: Với a ≠ 0; b ≠ 0; , ta có:
Hình ảnh tổng hợp các công thức lũy thừa quan trọng, giúp học sinh dễ dàng tra cứu và áp dụng khi giải bài tập.
Tính chất về bất đẳng thức:
- So sánh cùng cơ số: Cho . Khi đó:
- Với $a > 1$ thì
- Với $0<a<1$ thì
- Với số mũ âm $n<0$: