Để giải quyết các bài toán liên quan đến hàm logarit một cách chính xác và nhanh chóng, việc nắm vững lý thuyết và điều kiện hàm logarit là vô cùng quan trọng. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về điều kiện hàm logarit, giúp bạn tự tin chinh phục mọi dạng bài tập.
Ảnh này tóm tắt các kiến thức cơ bản về hàm số logarit và các điều kiện đi kèm để hàm số có nghĩa.
1. Nhắc Lại Về Logarit
1.1. Định Nghĩa Logarit
Logarit của một số là lũy thừa mà cơ số phải được nâng lên để tạo ra số đó. Nói cách khác, logarit là phép toán ngược của lũy thừa.
Ví dụ: Nếu $log_a b = y$ thì $a^y = b$.
Có nhiều loại logarit, bao gồm:
- Logarit thập phân: Cơ số 10 ($log_{10} b = log b = lg b$).
- Logarit tự nhiên: Cơ số e ($ln(b) = log_e b$).
- Logarit nhị phân: Cơ số 2 ($log_2 b$).
Công thức chung:
$log_a b$, với $b > 0$ và $0 < a neq 1$
1.2. Điều Kiện Để Logarit Có Nghĩa
Để logarit $log_a b$ có nghĩa, cần thỏa mãn hai điều kiện sau:
- Số $b$ phải dương: $b > 0$.
- Cơ số $a$ phải dương và khác 1: $0 < a neq 1$.
Nắm vững điều kiện này là nền tảng quan trọng để xác định điều kiện hàm logarit.
2. Hàm Logarit: Định Nghĩa và Điều Kiện
2.1. Định Nghĩa Hàm Logarit
Hàm logarit là hàm số có thể biểu diễn dưới dạng logarit. Với số thực $a > 0$ và $a neq 1$, hàm số $y = log_a x$ được gọi là hàm số logarit cơ số $a$.
Đồ thị của hàm logarit $y = log_a x$ có dạng như sau:
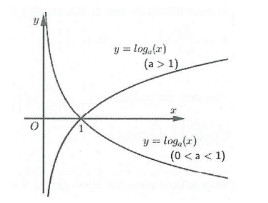Đồ thị hàm logarit với a > 1 và 0 < a < 1, thể hiện tính chất đồng biến và nghịch biến
Hình ảnh minh họa đồ thị của hàm logarit với hai trường hợp cơ số a lớn hơn 1 và a nhỏ hơn 1 nhưng lớn hơn 0, nhấn mạnh tính chất và hình dạng của đồ thị.
Đặc điểm của đồ thị hàm logarit:
- Tiệm cận đứng là trục $Oy$.
- Luôn đi qua điểm $(1; 0)$.
- Nằm bên phải trục tung.
Đồ thị hàm số $y = a^x$ và $y = log_a x$ (với $0 < a neq 1$) đối xứng nhau qua đường thẳng $y = x$.
2.2. Điều Kiện Hàm Logarit Tổng Quát
Xét hàm số $y = log_a x$, ta có các điều kiện hàm logarit sau:
- $a > 0$ và $a neq 1$.
- $x > 0$.
- Nếu hàm số có dạng $y = log_a [U(x)]$, thì điều kiện là $U(x) > 0$. Nếu $a$ chứa biến $x$, thì cần bổ sung điều kiện $0 < a neq 1$.
- Trường hợp đặc biệt: $y = log_a [U(x)]^n$. Điều kiện là $U(x) > 0$ nếu $n$ lẻ và $U(x) neq 0$ nếu $n$ chẵn.
Tổng quát, nếu có hàm số $y = log_{u(x)} v(x)$, thì điều kiện xác định là $v(x) > 0$ và $0 < u(x) neq 1$, đồng thời $u(x)$ phải xác định.
Hình ảnh này tổng hợp các điều kiện cần thiết để một hàm logarit có nghĩa, bao gồm điều kiện cho cơ số và biểu thức bên trong logarit.
2.3. Các Bước Tìm Điều Kiện Hàm Logarit
Để tìm điều kiện hàm logarit một cách nhanh chóng, hãy thực hiện theo các bước sau:
Xét hàm số $y = log_a u(x)$ (với $a > 0$ và $a neq 1$):
Bước 1: Tìm điều kiện xác định của hàm số $u(x)$.
Bước 2: Giải bất phương trình $u(x) > 0$.
Ví dụ 1: Tìm điều kiện xác định của hàm số $log_2 (sqrt{2} – 2)$.
$sqrt{2} – 2 < 0$. Do đó, hàm số không xác định.
Ảnh này minh họa một ví dụ cụ thể về cách áp dụng điều kiện của hàm logarit để xác định xem một biểu thức có nghĩa hay không.
Ví dụ 2: Tìm điều kiện của hàm logarit $y = log_{x-1} (x^2 – 3x + 2)$
Hình ảnh này minh họa cách xác định điều kiện của hàm logarit khi cả cơ số và biểu thức bên trong đều chứa biến x, cần phải giải các bất phương trình để tìm ra tập xác định.
- Điều kiện:
- $x – 1 > 0 Rightarrow x > 1$.
- $x – 1 neq 1 Rightarrow x neq 2$.
- $x^2 – 3x + 2 > 0 Rightarrow (x-1)(x-2) > 0 Rightarrow x < 1$ hoặc $x > 2$.
- Kết hợp các điều kiện trên, ta có $x > 2$.
3. Luyện Tập Với Bài Tập Áp Dụng
Để thành thạo việc xác định điều kiện hàm logarit, hãy luyện tập thường xuyên với các dạng bài tập khác nhau. Việc này giúp bạn nắm vững kiến thức và áp dụng một cách linh hoạt.
Nắm vững lý thuyết và thực hành giải các bài tập về điều kiện hàm logarit sẽ giúp bạn tự tin hơn trong quá trình học tập và giải quyết các bài toán liên quan. Chúc bạn thành công!