Hàm logarit là một khái niệm quan trọng trong toán học. Để hiểu và giải quyết các bài toán liên quan đến hàm logarit, việc nắm vững lý thuyết và các điều kiện xác định là vô cùng cần thiết. Bài viết này sẽ trình bày chi tiết về điều Kiện Hàm Logarit, kèm theo các ví dụ minh họa và bài tập áp dụng để bạn đọc có thể nắm vững kiến thức một cách hiệu quả.
Tổng quan về hàm số logarit, bao gồm định nghĩa, điều kiện cơ số và biểu thức dưới logarit, cần thiết để hàm số có nghĩa.
1. Ôn Tập Lý Thuyết Về Logarit
1.1. Định Nghĩa Logarit
Logarit của một số b là số mũ mà cơ số a phải được nâng lên để tạo ra số b đó. Phép toán logarit là phép toán nghịch đảo của lũy thừa.
Ví dụ: $log_a b = y$ tương đương với $a^y = b$. Logarit cơ số 10 của 1000 là 3, vì $10^3 = 1000$.
Các loại logarit thường gặp:
- Logarit thập phân: Cơ số 10, ký hiệu $log_{10}b = logb = lgb$.
- Logarit tự nhiên: Cơ số là hằng số e (≈ 2.718), ký hiệu $ln(b) = log_e b$.
- Logarit nhị phân: Cơ số 2, ký hiệu $log_2 b$.
Công thức chung: $log_a b$ với $b > 0$ và $0 < a neq 1$.
1.2. Điều Kiện Để Logarit Có Nghĩa
Để biểu thức logarit $log_a b$ có nghĩa, cần phải thỏa mãn đồng thời hai điều kiện sau:
- Số b phải dương: $b > 0$ (không có logarit của số âm).
- Cơ số a phải dương và khác 1: $0 < a neq 1$.
Việc nắm vững điều kiện này là tiền đề quan trọng để xác định điều kiện hàm logarit.
2. Hàm Logarit và Điều Kiện Của Hàm Logarit
2.1. Định Nghĩa Hàm Logarit
Hàm logarit là hàm số có dạng $y = log_a x$, trong đó a là một số thực dương khác 1 và x là biến số.
- Định nghĩa: Cho số thực $a > 0$, $a neq 1$. Hàm số $y = log_a x$ được gọi là hàm số logarit cơ số a.
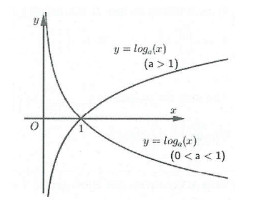
Đồ thị của hàm logarit $y = log_a x$ có những đặc điểm sau:
- Luôn đi qua điểm (1; 0).
- Có tiệm cận đứng là trục Oy.
- Nằm phía bên phải trục tung.
Minh họa đồ thị hàm logarit y = log_a(x) với a > 1 và 0 < a < 1, thể hiện sự khác biệt về tính đồng biến và nghịch biến.
Đồ thị hàm số $y = a^x$ và $y = log_a x$ đối xứng nhau qua đường thẳng $y = x$.
2.2. Điều Kiện Hàm Logarit Tổng Quát
Xét hàm số $y = log_a[U(x)]$, ta có các điều kiện sau:
- Điều kiện 1: $a > 0$ và $a neq 1$ (điều kiện của cơ số).
- Điều kiện 2: $U(x) > 0$ (biểu thức dưới logarit phải dương).
- Trường hợp đặc biệt: Nếu $y = log_a[U(x)]^n$, thì $U(x) > 0$ nếu n lẻ và $U(x) neq 0$ nếu n chẵn.
Tóm tắt điều kiện xác định cho hàm logarit y = log_u(x)(v(x)), nhấn mạnh u(x) > 0 và v(x) > 0, đồng thời u(x) phải xác định.
2.3. Các Bước Tìm Điều Kiện Hàm Logarit Kèm Ví Dụ
Để tìm điều kiện xác định của hàm logarit $y = log_a u(x)$ với $(a > 0, a neq 1)$, thực hiện các bước sau:
Bước 1: Tìm điều kiện để $u(x)$ xác định (nếu có).
Bước 2: Giải bất phương trình $u(x) > 0$.
Ví dụ 1: Tìm điều kiện xác định của hàm số $log_2(sqrt{2} – 2)$.
Vì $sqrt{2} – 2 < 0$ nên hàm số không xác định.
Ví dụ cụ thể về việc xác định điều kiện của hàm logarit, chỉ ra rằng biểu thức dưới logarit phải lớn hơn 0 để hàm số có nghĩa.
Ví dụ 2: Tìm điều kiện của hàm logarit $y = log_{x-1}(x^2 – 3x + 2)$.
Bài toán tìm điều kiện xác định của hàm logarit, yêu cầu biểu thức dưới logarit lớn hơn 0 và cơ số phải dương, khác 1.
Điều kiện:
- $x^2 – 3x + 2 > 0$
- $x – 1 > 0$
- $x – 1 neq 1$
Giải các bất phương trình và phương trình trên, ta được:
- $x < 1$ hoặc $x > 2$
- $x > 1$
- $x neq 2$
Kết hợp các điều kiện, ta có $x > 2$ và $x neq 2$, vậy $x > 2$.
3. Bài Tập Áp Dụng Về Điều Kiện Hàm Logarit
Để thành thạo việc xác định điều kiện hàm logarit, bạn cần luyện tập thường xuyên với nhiều dạng bài tập khác nhau. Dưới đây là một số bài tập bạn có thể tham khảo:
- Tìm điều kiện xác định của hàm số $y = log_3 (x^2 – 4x + 3)$.
- Tìm điều kiện xác định của hàm số $y = log_{x+2} (5 – x)$.
- Tìm điều kiện xác định của hàm số $y = log_x (x^2 – 1)$.
Lời khuyên: Hãy tự giải các bài tập này trước khi tham khảo đáp án. Việc tự mình giải quyết vấn đề sẽ giúp bạn hiểu sâu hơn về kiến thức và rèn luyện kỹ năng giải toán.
Hi vọng bài viết này đã cung cấp cho bạn đầy đủ kiến thức về điều kiện hàm logarit, từ lý thuyết cơ bản đến các ví dụ minh họa và bài tập áp dụng. Chúc bạn học tốt!