Hàm logarit là một khái niệm quan trọng trong chương trình toán học phổ thông và đại học. Để hiểu rõ và giải quyết các bài toán liên quan đến hàm logarit, việc nắm vững điều Kiện Của Hàm Logarit là vô cùng cần thiết. Bài viết này sẽ cung cấp một cái nhìn toàn diện về điều kiện của hàm logarit, từ định nghĩa cơ bản đến các ví dụ minh họa và bài tập áp dụng.
Ảnh: Bảng tổng hợp kiến thức về hàm số logarit, nhấn mạnh điều kiện xác định của hàm số để học sinh dễ dàng nắm bắt.
1. Ôn Tập Lý Thuyết Về Logarit
1.1. Định Nghĩa Logarit
Logarit là phép toán nghịch đảo của lũy thừa. Logarit của một số b (còn gọi là cơ số của logarit) là số mũ mà cơ số a (giá trị cố định) phải được nâng lên để tạo ra số b.
Ví dụ: $logab = y$ tương đương với $a^y = b$. Logarit cơ số 10 của 1000 là 3, vì $10^3 = 1000$, hay $log{10}1000 = 3$.
Các loại logarit phổ biến:
- Logarit thập phân: Cơ số 10, ký hiệu $log_{10}b = logb = lgb$.
- Logarit tự nhiên: Cơ số e (hằng số Euler), ký hiệu $ln(b) = log_e{b}$.
- Logarit nhị phân: Cơ số 2, ký hiệu $log_2b$.
Công thức chung của logarit:
$log_ab$, trong đó $b > 0$, $0 < a neq 1$
1.2. Điều Kiện Để Logarit Có Nghĩa
Để logarit $log_ab$ có nghĩa, cần thỏa mãn hai điều kiện sau:
- Số b phải dương: $b > 0$.
- Cơ số a phải dương và khác 1: $0 < a neq 1$.
Nắm vững hai điều kiện này là tiền đề quan trọng để hiểu điều kiện của hàm logarit.
2. Hàm Logarit và Điều Kiện Của Hàm Logarit
2.1. Định Nghĩa Hàm Logarit
Hàm logarit là hàm số có thể biểu diễn dưới dạng logarit. Hàm logarit cơ số a được định nghĩa như sau:
Cho số thực $a > 0$, $a neq 1$. Hàm số $y = log_ax$ được gọi là hàm số logarit cơ số a.
Đồ thị của hàm logarit $y = log_ax$ có dạng như sau:
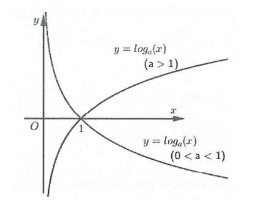Đồ thị hàm logarit – minh họa trực quan về tính chất và điều kiện của hàm logarit
Ảnh: Đồ thị hàm logarit, thể hiện rõ các đặc điểm như tiệm cận đứng, điểm đi qua và mối quan hệ với trục tung.
Nhận xét:
- Đồ thị hàm số có tiệm cận đứng là trục Oy và luôn đi qua điểm (1; 0) và nằm phía bên phải trục tung.
- Đồ thị hàm số $y = a^x$ và $y = log_ax$ (với $0 < a neq 1$) đối xứng nhau qua đường thẳng $y = x$.
2.2. Điều Kiện Hàm Logarit
Xét hàm số $y = log_ax$, ta có các điều kiện của hàm logarit như sau:
- $a > 0$
- $a neq 1$
- $x > 0$
Tổng quát:
- Với hàm số $y = log_a[U(x)]$, điều kiện là $U(x) > 0$. Nếu a chứa biến x, cần bổ sung điều kiện $0 < a neq 1$.
- Với hàm số $y = log_a[U(x)]^n$, điều kiện là $U(x) > 0$ nếu n lẻ, và $U(x) neq 0$ nếu n chẵn.
Ảnh: Sơ đồ hóa các điều kiện xác định của hàm logarit, giúp người học dễ dàng ghi nhớ và áp dụng.
2.3. Các Bước Tìm Điều Kiện Hàm Logarit Kèm Ví Dụ Minh Họa
Để tìm điều kiện của hàm logarit một cách nhanh chóng và chính xác, hãy thực hiện theo các bước sau:
Xét hàm số logarit $y = log_au(x)$ (với $a > 0$, $a neq 1$):
Bước 1: Tìm điều kiện xác định của $u(x)$.
Bước 2: Giải bất phương trình $u(x) > 0$.
Ví dụ 1: Tìm điều kiện xác định của hàm số $log_2(sqrt{2}-2)$.
Ta thấy $sqrt{2} – 2 < 0$. Do đó, hàm số không xác định vì biểu thức trong logarit phải lớn hơn 0.
Ảnh: Ví dụ minh họa cụ thể cách xác định điều kiện của hàm logarit với biểu thức số, giúp người đọc hiểu rõ hơn về quy trình.
Ví dụ 2: Tìm điều kiện của hàm logarit: $y = log_{x-1}(x^2 – 3x + 2)$
Điều kiện:
- $x – 1 > 0$
- $x – 1 neq 1$
- $x^2 – 3x + 2 > 0$
Giải các điều kiện trên, ta được:
- $x > 1$
- $x neq 2$
- $(x – 1)(x – 2) > 0$ => $x < 1$ hoặc $x > 2$
Kết hợp các điều kiện, ta được $x > 2$.
Ảnh: Ví dụ minh họa cách xác định điều kiện của hàm logarit với biểu thức chứa biến, yêu cầu kết hợp nhiều điều kiện.
3. Bài Tập Áp Dụng Về Điều Kiện Hàm Logarit
Để nắm vững kiến thức về điều kiện của hàm logarit, việc luyện tập là vô cùng quan trọng. Hãy tự giải các bài tập sau và so sánh với đáp án để củng cố kiến thức:
( Bài tập và đáp án chi tiết sẽ được cung cấp trong file đính kèm )
Hi vọng rằng bài viết này đã cung cấp cho bạn một cái nhìn toàn diện và sâu sắc về điều kiện của hàm logarit. Việc nắm vững lý thuyết và luyện tập thường xuyên sẽ giúp bạn tự tin chinh phục mọi bài toán liên quan đến hàm logarit.
