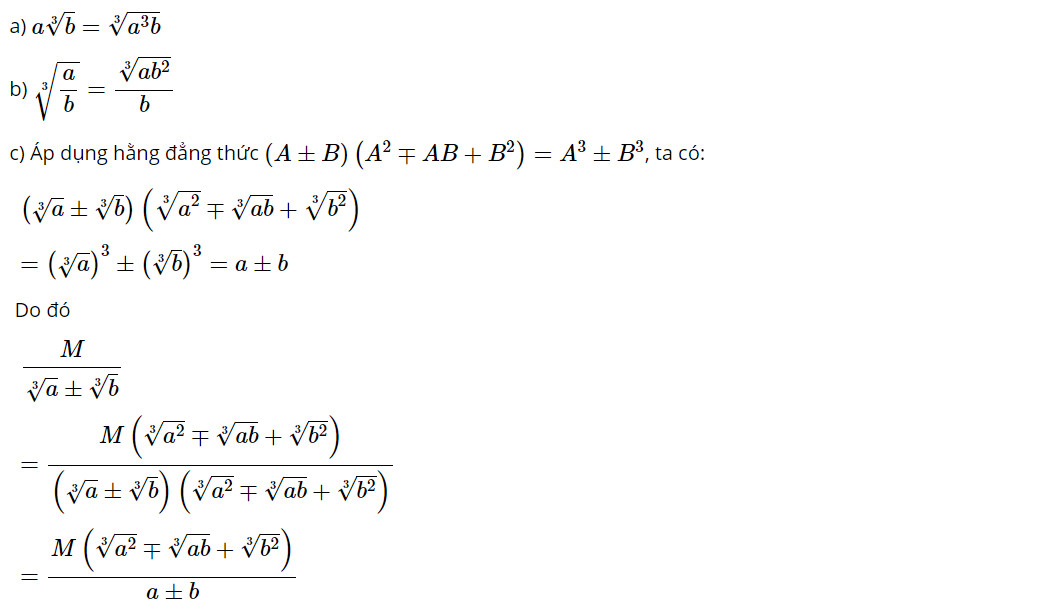Căn bậc 3 là một khái niệm toán học quan trọng, thường xuyên xuất hiện trong chương trình học phổ thông và các ứng dụng thực tế. Tuy nhiên, không phải ai cũng hiểu rõ về điều kiện tồn tại và các tính chất liên quan đến phép toán này. Bài viết này sẽ đi sâu vào phân tích các khía cạnh khác nhau của căn bậc 3, giúp bạn nắm vững kiến thức và áp dụng hiệu quả vào giải bài tập.
Tính Chất Cơ Bản Của Căn Bậc 3
Điểm khác biệt lớn nhất giữa căn bậc 3 và căn bậc 2 nằm ở điều kiện xác định. Trong khi căn bậc 2 chỉ có nghĩa khi biểu thức dưới dấu căn không âm (lớn hơn hoặc bằng 0), thì căn bậc 3 lại không bị ràng buộc bởi điều kiện này.
Điều này có nghĩa là: Căn bậc 3 của một số thực bất kỳ luôn tồn tại, kể cả khi số đó âm, dương hoặc bằng 0.
Ví dụ, ta có thể tính căn bậc 3 của -8, kết quả là -2, vì (-2) (-2) (-2) = -8. Điều này không thể thực hiện được với căn bậc 2, vì không có số thực nào bình phương lên lại cho kết quả âm.
Như vậy, việc khai căn bậc 3 đơn giản hơn nhiều so với căn bậc 2 do không cần xét dấu của giá trị dưới căn.
Áp Dụng Các Tính Chất Của Căn Bậc 3
Các tính chất của căn bậc 3 cho phép chúng ta biến đổi và đơn giản hóa các biểu thức phức tạp. Dưới đây là một số tính chất quan trọng:
- Căn bậc 3 của một tích: ³√(a b) = ³√a ³√b
- Căn bậc 3 của một thương: ³√(a / b) = ³√a / ³√b (với b ≠ 0)
- Lũy thừa của căn bậc 3: (³√a)^n = ³√(a^n)
Các tính chất này giúp chúng ta đưa thừa số vào trong căn, khai căn một biểu thức, khử mẫu của biểu thức lấy căn bậc ba hoặc trục căn bậc ba ở mẫu một cách dễ dàng.
Các Dạng Bài Tập Thường Gặp Về Căn Bậc 3
Để làm chủ kiến thức về căn bậc 3, chúng ta cần luyện tập với nhiều dạng bài tập khác nhau. Dưới đây là một số dạng bài thường gặp:
Dạng 1: Tính giá trị của căn bậc 3:
Yêu cầu tính giá trị của căn bậc 3 của một số thực hoặc một biểu thức số học. Để giải quyết dạng bài này, bạn cần nắm vững các tính chất cơ bản của căn bậc 3 và quy tắc đưa số vào/ra khỏi dấu căn.
Dạng 2: So sánh các căn bậc 3:
Yêu cầu so sánh giá trị của hai hay nhiều căn bậc 3. Để so sánh, bạn có thể đưa các biểu thức về cùng một dạng căn, hoặc sử dụng tính chất đồng biến của hàm số y = x³ để so sánh các số dưới dấu căn.
Dạng 3: Giải phương trình chứa căn bậc 3:
Đây là dạng bài tập phức tạp hơn, yêu cầu bạn áp dụng các kỹ năng biến đổi đại số và kiến thức về căn bậc 3 để giải phương trình. Các phương pháp thường được sử dụng bao gồm lập phương hai vế, đặt ẩn phụ hoặc phân tích thành nhân tử.
Bài Tập Thực Hành Về Căn Bậc 3
Để củng cố kiến thức, hãy cùng luyện tập một số bài tập sau:
Bài tập 1: Chứng minh giá trị của biểu thức sau không phụ thuộc vào biến x:
Hướng dẫn giải:
Bài tập 2: Giải phương trình sau:
Hướng dẫn giải:
Bài tập 3: Rút gọn các biểu thức sau:
Hướng dẫn giải:
Hy vọng rằng, qua bài viết này, bạn đã hiểu rõ hơn về điều Kiện Của Căn Bậc 3 và các ứng dụng của nó. Việc nắm vững kiến thức này sẽ giúp bạn tự tin hơn trong quá trình học tập và giải quyết các bài toán liên quan.