Tam giác đều là một hình học cơ bản và quan trọng, xuất hiện nhiều trong các bài toán và ứng dụng thực tế. Việc tính Diện Tích Tam Giác đều Cạnh A là một kỹ năng cần thiết. Bài viết này sẽ cung cấp công thức tính diện tích, chứng minh công thức và các ứng dụng liên quan.
Công thức tính diện tích tam giác đều
Diện tích (S) của một tam giác đều có cạnh bằng a được tính theo công thức sau:
S = (a² * √3) / 4
Chứng minh công thức diện tích tam giác đều
Công thức trên có thể được chứng minh bằng cách sử dụng định lý Pythagoras và kiến thức về đường cao trong tam giác đều.
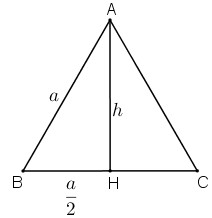
- Vẽ đường cao: Trong tam giác đều ABC, vẽ đường cao AH từ đỉnh A xuống cạnh BC. Vì ABC là tam giác đều, AH đồng thời là đường trung tuyến.
Hình ảnh minh họa tam giác đều ABC có cạnh a, đường cao AH, H là trung điểm của BC.
- Tính độ dài đường cao AH: Vì H là trung điểm của BC, nên BH = HC = a/2. Xét tam giác vuông AHB, áp dụng định lý Pythagoras:
AB² = AH² + BH²
a² = AH² + (a/2)²
a² = AH² + a²/4
AH² = a² – a²/4 = 3a²/4
AH = √(3a²/4) = (a√3)/2
- Tính diện tích: Diện tích tam giác ABC được tính bằng công thức:
S = (1/2) đáy chiều cao = (1/2) BC AH = (1/2) a (a√3)/2 = (a²√3)/4
Vậy, công thức tính diện tích tam giác đều cạnh a là S = (a²√3)/4.
Ứng dụng của công thức tính diện tích tam giác đều
Công thức tính diện tích tam giác đều cạnh a có nhiều ứng dụng trong các lĩnh vực khác nhau:
- Toán học: Giải các bài toán liên quan đến hình học phẳng, tính diện tích các hình phức tạp được tạo thành từ các tam giác đều.
- Xây dựng: Tính toán diện tích các bề mặt có hình dạng tam giác đều trong thiết kế và thi công công trình.
- Kiến trúc: Sử dụng trong thiết kế các chi tiết trang trí, các cấu trúc mái vòm, hoặc các yếu tố kiến trúc khác.
- Thiết kế đồ họa: Tạo ra các họa tiết, hình nền hoặc các yếu tố đồ họa dựa trên hình tam giác đều.
- Cắt gọt vật liệu: Tính toán lượng vật liệu cần thiết để cắt thành hình tam giác đều, ví dụ trong ngành may mặc hoặc chế tạo.
Hình ảnh minh họa BH = a/2 trong tam giác đều, cho thấy H là trung điểm của cạnh BC.
Ví dụ minh họa
Ví dụ 1: Tính diện tích của một tam giác đều có cạnh a = 5cm.
Áp dụng công thức: S = (a²√3)/4 = (5²√3)/4 = (25√3)/4 ≈ 10.83 cm².
Ví dụ 2: Một miếng đất hình tam giác đều có cạnh 10m. Tính diện tích miếng đất đó.
Áp dụng công thức: S = (a²√3)/4 = (10²√3)/4 = (100√3)/4 = 25√3 ≈ 43.3 m².
Các bài toán thường gặp về diện tích tam giác đều
- Tính diện tích khi biết cạnh: Đây là dạng bài tập cơ bản, chỉ cần áp dụng trực tiếp công thức.
- Tính cạnh khi biết diện tích: Cho diện tích S, tìm cạnh a bằng cách biến đổi công thức: a = √(4S/√3).
- Bài toán liên quan đến chu vi và diện tích: Kết hợp công thức tính chu vi (P = 3a) và diện tích để giải các bài toán phức tạp hơn.
- Bài toán thực tế: Ứng dụng công thức vào các tình huống thực tế như tính diện tích mái nhà, diện tích vật liệu cần thiết…
Hình ảnh minh họa công thức Pitago sử dụng để tìm chiều cao AH trong tam giác vuông AHB.
Lưu ý khi tính diện tích tam giác đều
- Đảm bảo đơn vị đo của cạnh và diện tích phải thống nhất.
- Sử dụng máy tính hoặc bảng giá trị lượng giác để tính căn bậc hai của 3 (√3 ≈ 1.732) nếu cần độ chính xác cao.
- Khi giải các bài toán phức tạp, nên vẽ hình minh họa để dễ hình dung và áp dụng công thức chính xác.
Kết luận
Việc nắm vững công thức và cách chứng minh diện tích tam giác đều cạnh a giúp bạn giải quyết các bài toán hình học một cách dễ dàng và hiệu quả. Hy vọng bài viết này cung cấp đầy đủ thông tin hữu ích cho bạn.