Diện Tích Ngũ Giác Đều: Công Thức, Ví Dụ và Ứng Dụng Thực Tế

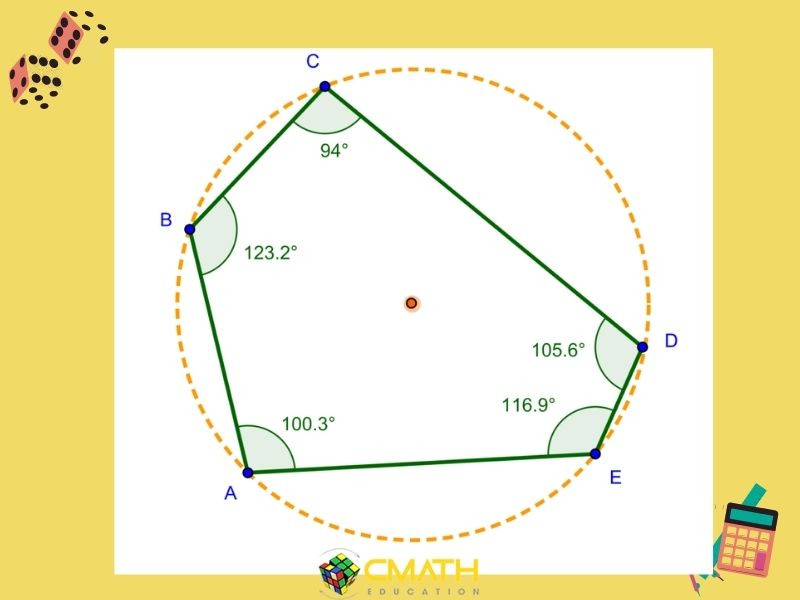
Hình ngũ giác là một hình đa giác với năm cạnh và năm góc. Ngũ giác có hai loại chính: ngũ giác đều (tất cả các cạnh và góc bằng nhau) và ngũ giác không đều (các cạnh và góc không bằng nhau). Bài viết này sẽ tập trung vào cách tính Diện Tích Ngũ Giác đều, cung cấp công thức, ví dụ minh họa và các ứng dụng thực tế.

Hình ảnh minh họa các loại hình ngũ giác, nhấn mạnh đặc điểm của ngũ giác đều với các cạnh và góc bằng nhau, khác biệt so với ngũ giác bất đều.

Công Thức Tính Diện Tích Ngũ Giác Đều

Ngũ giác đều là hình đa giác có năm cạnh bằng nhau và năm góc bằng nhau, mỗi góc có số đo là 108 độ. Để tính diện tích ngũ giác đều, chúng ta sử dụng công thức sau:

S = (5 * a^2) / (4 * tan(π/5))

Trong đó:

• S: Diện tích của ngũ giác đều.
• a: Độ dài một cạnh của ngũ giác đều.
• π: Số Pi (≈ 3.14159)
• tan: Hàm tang trong toán học.

Công thức này có thể được viết gọn hơn, sử dụng hằng số gần đúng:

S ≈ 1.72048 * a^2

Ví dụ:

Cho một ngũ giác đều có cạnh dài 5cm. Hãy tính diện tích ngũ giác đều này.

Áp dụng công thức:

S ≈ 1.72048 (5 cm)^2
S ≈ 1.72048 25 cm^2
S ≈ 43.012 cm^2

Vậy, diện tích ngũ giác đều có cạnh 5cm là khoảng 43.012 cm².

Hình vẽ ngũ giác đều với chú thích cạnh ‘a’ và công thức S ≈ 1.72048 * a^2, làm rõ cách áp dụng công thức tính diện tích.

Cách Tiếp Cận Khác Để Tính Diện Tích Ngũ Giác Đều

Ngoài công thức trực tiếp, bạn cũng có thể chia ngũ giác đều thành 5 tam giác cân bằng nhau, với đỉnh chung là tâm của ngũ giác. Khi đó:

1. Tính diện tích một tam giác cân.
2. Nhân diện tích này với 5 để được diện tích ngũ giác đều.

Để tính diện tích tam giác cân, bạn cần biết độ dài cạnh đáy (a) và chiều cao (khoảng cách từ tâm ngũ giác đến trung điểm của cạnh). Chiều cao này có thể được tính toán bằng các phương pháp lượng giác.

Ứng Dụng Của Diện Tích Ngũ Giác Đều Trong Thực Tế

Hình ngũ giác, đặc biệt là ngũ giác đều, có nhiều ứng dụng trong thực tế, bao gồm:

• Kiến trúc: Thiết kế các tòa nhà, cấu trúc có hình dáng độc đáo.
• Thiết kế: Tạo ra các hoa văn, họa tiết trang trí.
• Toán học và Khoa học: Nghiên cứu các tính chất hình học, ứng dụng trong các lĩnh vực khoa học khác.
• Sản xuất: Thiết kế các bộ phận máy móc có hình dạng ngũ giác.

Hình ảnh về ứng dụng hình học, có thể là một thiết kế kiến trúc, để minh họa tính ứng dụng của việc tính diện tích hình ngũ giác đều trong thực tế.

Hiểu và áp dụng công thức tính diện tích ngũ giác đều giúp chúng ta giải quyết nhiều vấn đề thực tế và khám phá vẻ đẹp của hình học trong cuộc sống.