Hình quạt tròn là một phần quan trọng trong hình học, xuất hiện nhiều trong các bài toán và ứng dụng thực tế. Bài viết này sẽ cung cấp kiến thức đầy đủ về diện tích hình quạt tròn, từ công thức cơ bản đến các dạng bài tập thường gặp, giúp bạn nắm vững và áp dụng hiệu quả.
Công Thức Tính Diện Tích Hình Quạt Tròn
Diện tích hình quạt tròn phụ thuộc vào bán kính và số đo cung của nó. Có hai công thức chính để tính diện tích hình quạt tròn:
1. Theo độ:
Nếu hình quạt tròn có bán kính R và cung có số đo n (độ), diện tích S của hình quạt tròn được tính bằng công thức:
S = (πR²n) / 360
2. Theo độ dài cung:
Nếu biết độ dài cung l của hình quạt tròn và bán kính R, diện tích S có thể được tính bằng công thức:
S = (lR) / 2
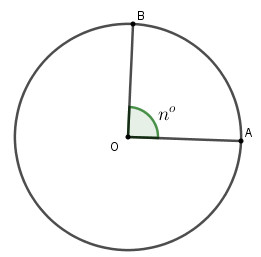
Hình ảnh minh họa hình quạt tròn, giúp người đọc hình dung và hiểu rõ hơn về các yếu tố liên quan đến công thức tính diện tích hình quạt. Trong đó chú thích rõ ràng bán kính (R) và số đo cung (n độ).
Các Dạng Toán Về Diện Tích Hình Quạt Tròn
Có hai dạng toán chính liên quan đến diện tích hình quạt tròn:
Dạng 1: Tính diện tích hình quạt tròn và các đại lượng liên quan
- Phương pháp: Sử dụng trực tiếp các công thức tính diện tích hình quạt tròn và hình tròn.
- Xác định các yếu tố đã biết: bán kính R, số đo cung n, độ dài cung l.
- Chọn công thức phù hợp và thay số để tính diện tích.
Dạng 2: Bài toán tổng hợp
- Phương pháp: Kết hợp các kiến thức hình học khác để giải quyết bài toán.
- Tính góc ở tâm hoặc bán kính đường tròn dựa trên các dữ kiện khác (ví dụ: tính chất tam giác, tứ giác).
- Áp dụng công thức tính diện tích hình quạt tròn sau khi đã tìm được các yếu tố cần thiết.
Bài Tập Vận Dụng
Dưới đây là một số bài tập vận dụng để bạn luyện tập và hiểu rõ hơn về cách tính diện tích hình quạt tròn:
Bài 1: Tính độ dài cung 30° của một đường tròn có bán kính 4 dm.
Giải:
Áp dụng công thức tính độ dài cung: l = (πRn) / 180 = (π * 4 * 30) / 180 = (2π) / 3 (dm)
Bài 2: Cho đường tròn (O) bán kính OA. Từ trung điểm M của OA vẽ dây BC ⊥ OA. Biết độ dài đường tròn (O) là 4π cm. Tính độ dài cung lớn BC.
Giải:
- Bán kính đường tròn:
R = 4π / (2π) = 2 cm. - ΔABO đều (chứng minh tương tự bài gốc) =>
∠AOB = 60° => ∠BOC = 120°. - Số đo cung lớn BC:
360° - 120° = 240°. - Độ dài cung lớn BC:
l = (π * 2 * 240) / 180 = (8π) / 3 cm.
Hình ảnh minh họa bài toán về đường tròn và dây cung, giúp người đọc dễ hình dung và tiếp cận bài toán một cách trực quan. Chú thích rõ ràng các điểm O, A, B, C và M trên hình vẽ.
Bài 3: Cho đường tròn (O, 10 cm), đường kính AB. Điểm M ∈ (O) sao cho ∠BAM = 45°. Tính diện tích hình quạt AOM.
Giải:
- ΔAOM vuông cân tại O =>
∠MOA = 90°. - Diện tích hình quạt AOM:
S = (π * 10² * 90) / 360 = 25π cm².
Hình ảnh minh họa bài toán liên quan đến góc nội tiếp và diện tích hình quạt, giúp người đọc dễ dàng hình dung vị trí các điểm và góc cần tính toán.
Bài 4: Cho đường tròn (O) đường kính AB = 4√3 cm. Điểm C ∈ (O) sao cho ∠ABC = 30°. Tính diện tích hình viên phân AC.
Giải:
∠AOC = 2 * ∠ABC = 60°=>S_qAOC = (πR²) / 6.- ΔAOC đều cạnh R. Gọi CH là đường cao =>
CH = (√3 / 2) * R => S_AOC = (√3 / 4) * R². - Diện tích hình viên phân AC:
(πR²) / 6 - (√3 / 4) * R² = (2π - 3√3) / 12 * (2√3)² = 2π - 3√3 cm².
Hình ảnh minh họa bài toán tính diện tích hình viên phân, giúp người đọc hiểu rõ hơn về khái niệm và cách tính toán liên quan đến hình viên phân.
Bài 5: Tại một vòng xoay ngã tư, người ta cần làm các bồn trồng hoa. Tính phần diện tích của 1 bồn hoa. Biết rằng bán kính của vòng tròn lớn là 7m, vòng tròn nhỏ là 3m, số đo cung tròn đó là 60°.
Giải:
- Diện tích hình quạt tròn lớn:
(π * 7² * 60) / 360 = (49π) / 6 m². - Diện tích hình quạt tròn nhỏ:
(π * 3² * 60) / 360 = (3π) / 2 m². - Diện tích phần bồn hoa:
(49π) / 6 - (3π) / 2 = (20π) / 3 ≈ 20.9 m².
Hình ảnh minh họa ứng dụng thực tế của hình quạt tròn trong thiết kế bồn hoa, giúp người đọc thấy được sự liên hệ giữa kiến thức hình học và đời sống.
Ứng Dụng Thực Tế của Diện Tích Hình Quạt Tròn
Diện tích hình quạt tròn có nhiều ứng dụng trong thực tế, ví dụ như:
- Kiến trúc và xây dựng: Tính diện tích các chi tiết trang trí hình quạt, thiết kế mái vòm.
- Thiết kế: Thiết kế các vật dụng hình quạt như quạt giấy, đèn trang trí.
- Nông nghiệp: Tính diện tích tưới tiêu của hệ thống phun nước hình quạt.
- Toán học và khoa học: Giải các bài toán liên quan đến chuyển động tròn, tính diện tích bề mặt cong.
Hình ảnh minh họa một ứng dụng thực tế, máy kéo nông nghiệp với kích thước bánh xe khác nhau liên quan đến chu vi hình tròn và số vòng quay.
Nắm vững công thức và luyện tập các bài tập về diện tích hình quạt tròn sẽ giúp bạn giải quyết các bài toán hình học một cách dễ dàng và ứng dụng kiến thức này vào thực tế một cách hiệu quả.