Điểm cực tiểu của hàm số là một khái niệm quan trọng trong giải tích, giúp xác định các giá trị nhỏ nhất “tương đối” của hàm số trong một khoảng nhất định. Việc nắm vững định nghĩa, cách tìm và ứng dụng của điểm cực tiểu là rất cần thiết trong học tập và nghiên cứu toán học, cũng như trong các bài toán thực tế.
Định Nghĩa Điểm Cực Tiểu
Cho hàm số $y = f(x)$ xác định trên khoảng $(a; b)$ và $x_0 in (a; b)$.
- $x_0$ được gọi là điểm Cực Tiểu Của Hàm Số $f(x)$ nếu tồn tại một khoảng $(x_0 – delta; x_0 + delta) subset (a; b)$ sao cho $f(x) > f(x_0)$, $forall x in (x_0 – delta; x_0 + delta) setminus {x_0}$.
- Giá trị $f(x_0)$ được gọi là giá trị cực tiểu của hàm số.
Lưu ý: Điểm cực tiểu là giá trị $x$, còn giá trị cực tiểu là giá trị $y = f(x)$ tại điểm cực tiểu đó.
Điều Kiện Cần và Đủ để Hàm Số Có Điểm Cực Tiểu
Điều kiện cần: Nếu hàm số $f(x)$ đạt cực tiểu tại $x_0$ và có đạo hàm tại điểm đó thì $f'(x_0) = 0$.
Điều kiện đủ:
- Cách 1: Nếu $f'(x)$ đổi dấu từ âm sang dương khi $x$ đi qua $x_0$ thì $x_0$ là điểm cực tiểu của hàm số $f(x)$.
- Cách 2: Nếu $f'(x_0) = 0$ và $f”(x_0) > 0$ thì $x_0$ là điểm cực tiểu của hàm số $f(x)$.
Phương Pháp Tìm Điểm Cực Tiểu của Hàm Số
Để tìm điểm cực tiểu của hàm số $y = f(x)$, ta thực hiện các bước sau:
- Tìm tập xác định của hàm số.
- Tính đạo hàm $f'(x)$.
- Tìm các điểm $x_i$ mà tại đó $f'(x_i) = 0$ hoặc $f'(x_i)$ không xác định.
- Lập bảng biến thiên của hàm số.
- Dựa vào bảng biến thiên, xác định các điểm cực tiểu của hàm số.
Hoặc, ta có thể sử dụng cách sau:
- Tính đạo hàm $f'(x)$ và tìm các nghiệm $x_i$ của phương trình $f'(x) = 0$.
- Tính đạo hàm bậc hai $f”(x)$.
- Xét dấu của $f”(x_i)$ tại các nghiệm $x_i$ tìm được. Nếu $f”(x_i) > 0$ thì $x_i$ là điểm cực tiểu của hàm số.
Ví Dụ Minh Họa
Ví dụ 1: Cho hàm số có đồ thị như hình vẽ. Tìm điểm cực tiểu của hàm số.
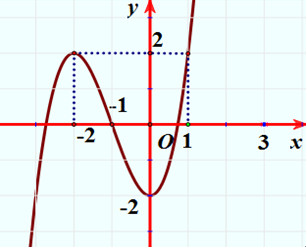
Alt text: Đồ thị hàm số minh họa điểm cực tiểu, trục hoành Ox và trục tung Oy.
Dựa vào đồ thị, ta thấy hàm số đạt cực tiểu tại $x = 0$. Vậy, điểm cực tiểu của hàm số là $x = 0$.
Ví dụ 2: Tìm điểm cực tiểu của hàm số $y = x^3 – 3x^2 + 1$.
- Tập xác định: $D = mathbb{R}$.
- $y’ = 3x^2 – 6x$.
- $y’ = 0 Leftrightarrow 3x^2 – 6x = 0 Leftrightarrow x = 0$ hoặc $x = 2$.
- $y” = 6x – 6$.
- $y”(0) = -6 < 0$ nên $x = 0$ là điểm cực đại.
$y”(2) = 6 > 0$ nên $x = 2$ là điểm cực tiểu.
Vậy, điểm cực tiểu của hàm số là $x = 2$.
Bảng biến thiên của hàm số có dạng như sau:
Alt text: Bảng biến thiên của hàm số bậc ba, minh họa điểm cực đại và cực tiểu.
Ứng Dụng của Điểm Cực Tiểu
- Tối ưu hóa: Điểm cực tiểu được sử dụng để tìm giá trị nhỏ nhất của một hàm số, có ứng dụng trong nhiều lĩnh vực như kinh tế (tối thiểu chi phí), kỹ thuật (tối ưu hóa thiết kế),…
- Vẽ đồ thị hàm số: Xác định điểm cực tiểu giúp vẽ đồ thị hàm số chính xác hơn.
- Giải các bài toán liên quan: Điểm cực tiểu là kiến thức nền tảng để giải nhiều bài toán liên quan đến hàm số, bất đẳng thức,…
Nắm vững kiến thức về điểm cực tiểu của hàm số giúp học sinh và người học có thể giải quyết các bài toán liên quan một cách hiệu quả và chính xác. Đồng thời, kiến thức này còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau của đời sống.
