Điểm cực tiểu của đồ thị hàm số là một khái niệm quan trọng trong giải tích, giúp chúng ta hiểu rõ hơn về hình dạng và đặc tính của đồ thị hàm số. Trong bài viết này, chúng ta sẽ đi sâu vào định nghĩa, cách xác định và ứng dụng của điểm cực tiểu, cùng với ví dụ minh họa cụ thể.
Định nghĩa điểm Cực Tiểu Của đồ Thị Hàm Số
Cho hàm số y = f(x) xác định trên khoảng (a; b) và x₀ ∈ (a; b).
- Điểm x₀ được gọi là điểm cực tiểu của hàm số f(x) nếu tồn tại một khoảng (c; d) ⊂ (a; b) chứa x₀ sao cho f(x) ≥ f(x₀) với mọi x ∈ (c; d).
- Điểm (x₀; f(x₀)) được gọi là điểm cực tiểu của đồ thị hàm số y = f(x).
Điều kiện cần và đủ để hàm số có điểm cực tiểu
-
Điều kiện cần: Nếu hàm số f(x) đạt cực tiểu tại x₀ và có đạo hàm tại điểm đó thì f'(x₀) = 0.
-
Điều kiện đủ:
- Nếu f'(x₀) = 0 và f”(x₀) > 0 thì x₀ là điểm cực tiểu của hàm số f(x).
- Nếu f'(x) đổi dấu từ âm sang dương khi x đi qua x₀ thì x₀ là điểm cực tiểu của hàm số f(x).
Các bước tìm điểm cực tiểu của đồ thị hàm số
- Tìm tập xác định của hàm số.
- Tính đạo hàm bậc nhất f'(x).
- Giải phương trình f'(x) = 0 để tìm các điểm tới hạn xᵢ.
- Tính đạo hàm bậc hai f”(x) và xét dấu của f”(xᵢ). Nếu f”(xᵢ) > 0 thì xᵢ là điểm cực tiểu. Hoặc, xét dấu của f'(x) khi x đi qua xᵢ. Nếu f'(x) đổi dấu từ âm sang dương thì xᵢ là điểm cực tiểu.
- Tính giá trị của hàm số tại các điểm cực tiểu: yᵢ = f(xᵢ).
- Kết luận các điểm cực tiểu của đồ thị hàm số là (xᵢ; yᵢ).
Ví dụ minh họa
Xét hàm số y = x³ – 3x + 5. Tìm điểm cực tiểu của đồ thị hàm số này.
- Tập xác định: D = ℝ.
- Đạo hàm bậc nhất: y’ = 3x² – 3.
- Giải phương trình y’ = 0: 3x² – 3 = 0 ⇔ x² = 1 ⇔ x = ±1.
- Đạo hàm bậc hai: y” = 6x.
- Tại x = 1: y”(1) = 6 > 0. Vậy x = 1 là điểm cực tiểu.
- Tại x = -1: y”(-1) = -6 < 0. Vậy x = -1 là điểm cực đại.
- Tính giá trị hàm số tại x = 1: y(1) = 1³ – 3(1) + 5 = 3.
- Vậy điểm cực tiểu của đồ thị hàm số là (1; 3).
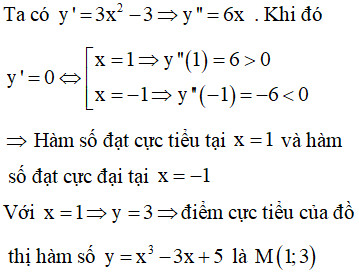
Đồ thị hàm số y = x³ – 3x + 5 minh họa điểm cực tiểu (1; 3). Đồ thị cho thấy sự biến thiên của hàm số và điểm thấp nhất tại x=1.
Ứng dụng của điểm cực tiểu trong thực tế
Việc tìm điểm cực tiểu của đồ thị hàm số không chỉ là một bài toán lý thuyết mà còn có nhiều ứng dụng thực tế, ví dụ:
- Tối ưu hóa chi phí: Trong kinh doanh, việc tìm điểm cực tiểu của hàm chi phí giúp doanh nghiệp xác định mức sản lượng tối ưu để giảm thiểu chi phí sản xuất.
- Thiết kế kỹ thuật: Trong kỹ thuật, việc tìm điểm cực tiểu của các hàm liên quan đến năng lượng hoặc vật liệu giúp thiết kế các công trình hoặc sản phẩm tiết kiệm và hiệu quả hơn.
- Dự báo và phân tích: Trong khoa học dữ liệu, điểm cực tiểu có thể đại diện cho các trạng thái ổn định hoặc các điểm quan trọng trong quá trình phát triển của một hệ thống.
Lưu ý khi tìm điểm cực tiểu
- Luôn kiểm tra điều kiện cần và đủ để đảm bảo điểm tìm được thực sự là điểm cực tiểu.
- Đối với các hàm số phức tạp, việc giải phương trình đạo hàm bằng 0 có thể khó khăn, cần sử dụng các phương pháp số hoặc công cụ hỗ trợ.
- Khi xét dấu đạo hàm bậc hai, cần chú ý đến các trường hợp đặc biệt như đạo hàm bậc hai bằng 0 hoặc không xác định.
Hiểu rõ về điểm cực tiểu của đồ thị hàm số là một bước quan trọng để nắm vững kiến thức về giải tích và ứng dụng nó vào các bài toán thực tế. Hy vọng bài viết này đã cung cấp cho bạn cái nhìn tổng quan và chi tiết về chủ đề này.
