Đường trung tuyến là một khái niệm quan trọng trong hình học, đặc biệt là trong tam giác. Hiểu rõ về đường trung tuyến giúp học sinh nắm vững kiến thức cơ bản và ứng dụng vào giải các bài toán liên quan. Vậy, đường trung tuyến là gì và có những tính chất, công thức nào cần lưu ý?
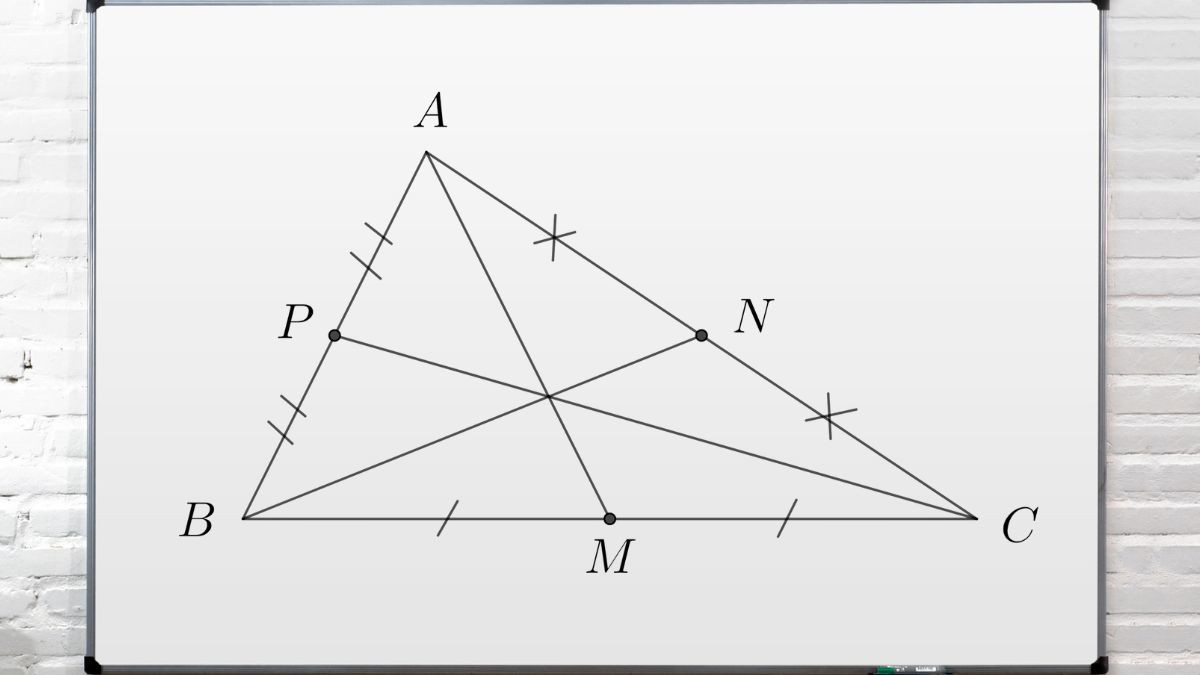
Đường trung tuyến của một tam giác là đoạn thẳng nối một đỉnh của tam giác đó với trung điểm của cạnh đối diện. Mỗi tam giác có ba đường trung tuyến, mỗi đường ứng với một đỉnh.
Hình ảnh minh họa các đường trung tuyến trong một tam giác, với mỗi đường nối một đỉnh tới trung điểm cạnh đối diện.
Công Thức Tính Độ Dài Đường Trung Tuyến
Để tính độ dài đg Trung Tuyến, ta có thể sử dụng công thức dựa trên định lý Apollonius. Cho tam giác ABC có các cạnh a, b, c lần lượt là BC, CA, AB. Gọi ma, mb, mc là độ dài các đường trung tuyến ứng với các cạnh a, b, c.
Khi đó, ta có các công thức sau:
- ma² = (2b² + 2c² – a²) / 4
- mb² = (2a² + 2c² – b²) / 4
- mc² = (2a² + 2b² – c²) / 4
Ảnh chụp công thức tính độ dài đường trung tuyến ma, mb, mc trong tam giác dựa trên độ dài ba cạnh a, b, c.
Tính Chất Quan Trọng Của Đường Trung Tuyến
Đg trung tuyến không chỉ là một đoạn thẳng đơn thuần mà còn mang nhiều tính chất quan trọng, giúp giải quyết các bài toán hình học một cách hiệu quả:
- Đồng quy: Ba đường trung tuyến của một tam giác đồng quy tại một điểm, điểm này được gọi là trọng tâm của tam giác.
- Trọng tâm chia đường trung tuyến: Trọng tâm của tam giác chia mỗi đường trung tuyến thành hai đoạn, trong đó đoạn nối từ đỉnh đến trọng tâm bằng 2/3 độ dài đường trung tuyến đó.
- Diện tích: Đường trung tuyến chia tam giác thành hai tam giác có diện tích bằng nhau. Đặc biệt, ba đường trung tuyến chia tam giác thành sáu tam giác nhỏ có diện tích bằng nhau.
- Tam giác vuông: Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.
Hình ảnh minh họa khái niệm đường trung tuyến trong tam giác, nhấn mạnh vai trò và tính chất của nó trong giải toán hình học.
Ứng Dụng Của Đường Trung Tuyến
Hiểu và vận dụng thành thạo các kiến thức về đg trung tuyến giúp học sinh giải quyết nhiều bài toán hình học, từ đơn giản đến phức tạp. Các bài toán thường gặp liên quan đến đường trung tuyến bao gồm:
- Chứng minh các đường thẳng đồng quy.
- Tính diện tích tam giác.
- Xác định vị trí trọng tâm của tam giác.
- Giải các bài toán liên quan đến tam giác vuông.
Nắm vững kiến thức về đường trung tuyến là nền tảng quan trọng giúp học sinh học tốt môn Toán và phát triển tư duy logic, khả năng giải quyết vấn đề.