Tứ giác nội tiếp là một khái niệm quan trọng trong chương trình hình học lớp 9, thường xuất hiện trong các bài kiểm tra và kỳ thi. Hiểu rõ Dấu Hiệu Tứ Giác Nội Tiếp sẽ giúp bạn giải quyết các bài toán liên quan một cách dễ dàng và chính xác. Bài viết này sẽ cung cấp kiến thức đầy đủ, chi tiết về tứ giác nội tiếp, giúp bạn nắm vững các dấu hiệu nhận biết và áp dụng chúng vào giải bài tập.
Tứ Giác Nội Tiếp Là Gì?
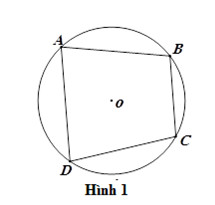
Tứ giác nội tiếp (còn gọi là tứ giác nội tiếp đường tròn) là tứ giác có tất cả bốn đỉnh nằm trên một đường tròn. Đường tròn này được gọi là đường tròn ngoại tiếp tứ giác.
Alt: Hình ảnh minh họa tứ giác nội tiếp ABCD trong đường tròn tâm O, thể hiện mối quan hệ giữa các đỉnh và đường tròn.
Định lý thuận: Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 180 độ.
Định lý đảo: Nếu một tứ giác có tổng số đo hai góc đối diện bằng 180 độ thì tứ giác đó là tứ giác nội tiếp.
Các Tính Chất Quan Trọng Của Tứ Giác Nội Tiếp
Nắm vững các tính chất sau đây sẽ giúp bạn nhận biết và chứng minh một tứ giác là nội tiếp:
- Tổng hai góc đối của tứ giác nội tiếp bằng 180 độ.
- Góc ngoài tại một đỉnh của tứ giác nội tiếp bằng góc trong của đỉnh đối diện.
- Mọi tam giác đều có một đường tròn ngoại tiếp.
- Bốn đỉnh của tứ giác nội tiếp cách đều tâm của đường tròn ngoại tiếp.
Các Dấu Hiệu Nhận Biết Tứ Giác Nội Tiếp
Đây là phần quan trọng nhất, giúp bạn xác định một tứ giác có phải là nội tiếp hay không:
-
Bốn đỉnh cách đều một điểm: Nếu tồn tại một điểm O sao cho OA = OB = OC = OD, thì tứ giác ABCD là tứ giác nội tiếp, với O là tâm đường tròn ngoại tiếp.
Alt: Hình minh họa chứng minh tứ giác nội tiếp khi 4 đỉnh A, B, C, D cách đều điểm I, với I là tâm đường tròn.
-
Tổng hai góc đối bằng 180 độ: Nếu tứ giác ABCD có ∠A + ∠C = 180° hoặc ∠B + ∠D = 180°, thì ABCD là tứ giác nội tiếp.
Alt: Tứ giác ABCD nội tiếp khi tổng góc A và góc C bằng 180 độ, một dấu hiệu quan trọng để nhận biết.
-
Góc ngoài tại một đỉnh bằng góc trong đỉnh đối: Nếu góc ngoài tại đỉnh A của tứ giác ABCD bằng góc C, thì tứ giác ABCD là tứ giác nội tiếp.
Alt: Hình ảnh minh họa góc ngoài tại đỉnh A bằng góc trong tại đỉnh C, một dấu hiệu chứng minh tứ giác nội tiếp.
-
Hai đỉnh kề nhau cùng nhìn một cạnh dưới một góc bằng nhau: Nếu hai đỉnh B và C cùng nhìn cạnh AD dưới một góc α, thì tứ giác ABCD là tứ giác nội tiếp.
-
Tứ giác đặc biệt: Hình chữ nhật, hình vuông là các tứ giác nội tiếp.
Alt: Hình chữ nhật là một ví dụ về tứ giác đặc biệt luôn nội tiếp được đường tròn.
Các Phương Pháp Chứng Minh Tứ Giác Nội Tiếp
Dựa vào các dấu hiệu trên, ta có các phương pháp chứng minh tứ giác nội tiếp như sau:
- Chứng minh bốn đỉnh cách đều một điểm: Xác định tâm O và chứng minh OA = OB = OC = OD.
- Chứng minh tổng hai góc đối bằng 180 độ: Tính toán và chứng minh ∠A + ∠C = 180° hoặc ∠B + ∠D = 180°.
- Chứng minh góc ngoài bằng góc trong đối: Chứng minh góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.
- Chứng minh hai đỉnh kề cùng nhìn một cạnh dưới một góc bằng nhau: Chứng minh hai góc tạo bởi hai đỉnh kề và một cạnh bằng nhau.
Bài Tập Vận Dụng Về Dấu Hiệu Tứ Giác Nội Tiếp
Để hiểu rõ hơn về cách áp dụng các dấu hiệu tứ giác nội tiếp, hãy cùng xem xét một số ví dụ sau:
Bài 1: Cho tam giác ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H. Chứng minh rằng tứ giác BFEC nội tiếp.
Giải:
Xét tứ giác BFEC có:
- ∠BFC = 90° (CF là đường cao)
- ∠BEC = 90° (BE là đường cao)
=> ∠BFC + ∠BEC = 180°
Vậy tứ giác BFEC nội tiếp (tổng hai góc đối bằng 180°).
Alt: Minh họa bài toán chứng minh tứ giác BFEC nội tiếp trong tam giác ABC có các đường cao cắt nhau tại H.
Bài 2: Cho đường tròn (O) và dây cung AB. Lấy điểm C thuộc cung lớn AB. Gọi D, E lần lượt là hình chiếu của C trên AB, OA. Chứng minh rằng tứ giác ADCE nội tiếp.
Giải:
Xét tứ giác ADCE có:
- ∠ADC = 90° (CD ⊥ AB)
- ∠AEC = 90° (CE ⊥ OA)
=> ∠ADC + ∠AEC = 180°
Vậy tứ giác ADCE nội tiếp (tổng hai góc đối bằng 180°).
Bài 3: Cho hình thang ABCD (AB // CD). Chứng minh rằng nếu ABCD là hình thang cân thì tứ giác ABCD nội tiếp.
Giải:
Vì ABCD là hình thang cân nên ∠A = ∠B và ∠C = ∠D.
Mà ∠A + ∠D = 180° (hai góc trong cùng phía)
=> ∠B + ∠C = 180°
Vậy tứ giác ABCD nội tiếp (tổng hai góc đối bằng 180°).
Alt: Hình thang cân ABCD, với góc C = D = 60 độ và CD = 2AD, chứng minh rằng nó nội tiếp một đường tròn.
Lưu Ý Quan Trọng Khi Giải Bài Tập Về Tứ Giác Nội Tiếp
- Vẽ hình chính xác: Hình vẽ đúng giúp bạn dễ dàng nhận ra các mối quan hệ hình học và áp dụng đúng dấu hiệu tứ giác nội tiếp.
- Ghi rõ giả thiết, kết luận: Điều này giúp bạn hệ thống hóa thông tin và xác định mục tiêu chứng minh.
- Sử dụng linh hoạt các phương pháp: Không phải bài toán nào cũng chỉ có một cách giải. Hãy thử nhiều cách tiếp cận để tìm ra lời giải tối ưu.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại các bước chứng minh để đảm bảo tính chính xác.
Kết Luận
Nắm vững các dấu hiệu tứ giác nội tiếp là chìa khóa để giải quyết các bài toán hình học liên quan. Hy vọng bài viết này đã cung cấp cho bạn kiến thức đầy đủ và hữu ích để tự tin chinh phục các bài tập về tứ giác nội tiếp. Chúc bạn học tốt!