Hình tứ giác là một hình học quen thuộc, nhưng để nhận biết và phân loại chúng một cách chính xác, chúng ta cần nắm vững các dấu hiệu đặc trưng. Bài viết này sẽ cung cấp một cái nhìn toàn diện về các Dấu Hiệu Nhận Biết Tứ Giác, giúp bạn dễ dàng xác định và giải quyết các bài toán liên quan.
I. Các Loại Tứ Giác Cơ Bản
Trước khi đi sâu vào các dấu hiệu nhận biết tứ giác đặc biệt, hãy cùng điểm qua các loại tứ giác cơ bản:
- Tứ giác đơn: Là tứ giác mà không có cạnh nào giao nhau.
- Tứ giác lồi: Là tứ giác mà tất cả các góc trong đều nhỏ hơn 180° và hai đường chéo nằm bên trong tứ giác.
- Tứ giác lõm: Là tứ giác có một góc trong lớn hơn 180° và một trong hai đường chéo nằm bên ngoài tứ giác.
- Tứ giác không đều: Là tứ giác không có cặp cạnh nào song song.
II. Dấu Hiệu Nhận Biết Các Hình Tứ Giác Đặc Biệt
Các hình tứ giác đặc biệt có những tính chất và dấu hiệu nhận biết riêng biệt, giúp chúng ta dễ dàng phân biệt chúng.
1. Hình Thang
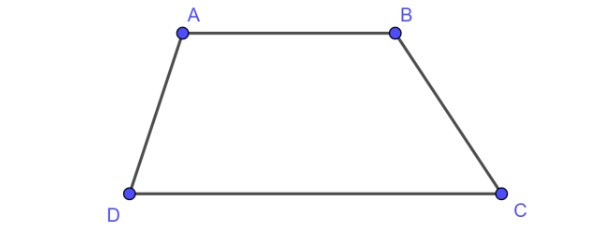
Định nghĩa: Hình thang là tứ giác có ít nhất một cặp cạnh đối song song.
Alt: Hình thang ABCD với AB song song CD, minh họa dấu hiệu nhận biết hình thang
2. Hình Thang Vuông
Định nghĩa: Hình thang vuông là hình thang có ít nhất một góc vuông.
Dấu hiệu nhận biết:
- Tứ giác có một cặp cạnh đối song song và một góc vuông.
- Tứ giác có ít nhất hai góc vuông.
3. Hình Thang Cân
Định nghĩa: Hình thang cân là hình thang có hai góc kề một cạnh đáy bằng nhau và hai đường chéo bằng nhau.
Dấu hiệu nhận biết:
- Hình thang có hai góc kề một cạnh đáy bằng nhau.
- Hình thang có hai đường chéo bằng nhau.
Alt: Hình thang cân ABCD với góc A bằng góc B và AC bằng BD, thể hiện tính chất hình thang cân
4. Hình Bình Hành
Định nghĩa: Hình bình hành là tứ giác có hai cặp cạnh đối song song.
Dấu hiệu nhận biết:
- Tứ giác có hai cặp cạnh đối song song.
- Tứ giác có các cạnh đối bằng nhau.
- Tứ giác có các góc đối bằng nhau.
- Tứ giác có một cặp cạnh đối song song và bằng nhau.
- Tứ giác có hai đường chéo giao nhau tại trung điểm của mỗi đường.
5. Hình Thoi
Định nghĩa: Hình thoi là tứ giác có bốn cạnh bằng nhau.
Dấu hiệu nhận biết:
- Tứ giác có bốn cạnh bằng nhau.
- Tứ giác có hai đường chéo là đường phân giác của cả bốn góc trong.
- Tứ giác có hai đường chéo là đường trung trực của nhau.
- Hình bình hành có hai cạnh kề bằng nhau.
- Hình bình hành có hai đường chéo vuông góc với nhau.
- Hình bình hành có một đường chéo là đường phân giác của một góc.
Alt: Hình thoi ABCD với AB=BC=CD=DA, minh họa tính chất các cạnh bằng nhau của hình thoi
6. Hình Chữ Nhật
Định nghĩa: Hình chữ nhật là tứ giác có bốn góc vuông.
Dấu hiệu nhận biết:
- Tứ giác có ba góc vuông.
- Hình thang cân có một góc vuông.
- Hình bình hành có một góc vuông.
- Hình bình hành có hai đường chéo bằng nhau.
7. Hình Vuông
Định nghĩa: Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.
Dấu hiệu nhận biết:
- Hình chữ nhật có hai cạnh kề bằng nhau.
- Hình chữ nhật có hai đường chéo vuông góc với nhau.
- Hình thoi có một góc vuông.
- Hình thoi có hai đường chéo bằng nhau.
Alt: Hình vuông ABCD với AB=BC=CD=DA và các góc vuông, biểu thị đầy đủ tính chất của hình vuông
III. Phương Pháp Chứng Minh Tứ Giác Đặc Biệt
Để chứng minh một tứ giác là một hình đặc biệt, chúng ta thường sử dụng các phương pháp sau:
- Chứng minh dựa vào định nghĩa: Chứng minh tứ giác thỏa mãn định nghĩa của hình đó.
- Chứng minh dựa vào dấu hiệu nhận biết: Chứng minh tứ giác có các dấu hiệu nhận biết của hình đó.
- Sử dụng tính chất bắc cầu: Chứng minh tứ giác là một hình đặc biệt khác, sau đó suy ra nó thuộc loại hình cần chứng minh.
Ví dụ, để chứng minh một tứ giác là hình bình hành, bạn có thể chứng minh nó có hai cặp cạnh đối song song, hoặc một cặp cạnh đối song song và bằng nhau, hoặc hai đường chéo cắt nhau tại trung điểm mỗi đường.
IV. Bài Tập Vận Dụng
Để củng cố kiến thức, hãy thử sức với một số bài tập sau:
- Cho tứ giác ABCD có AB // CD và $angle A = angle B$. Chứng minh rằng ABCD là hình thang cân.
- Cho hình bình hành ABCD. Gọi E và F lần lượt là trung điểm của AB và CD. Chứng minh rằng AECF là hình bình hành.
- Cho hình chữ nhật ABCD. Chứng minh rằng các đường trung trực của các cạnh của hình chữ nhật đồng quy tại một điểm.
Lời kết:
Nắm vững các dấu hiệu nhận biết tứ giác là một kỹ năng quan trọng trong học toán. Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và chi tiết về các loại tứ giác và cách nhận biết chúng. Chúc bạn học tốt!