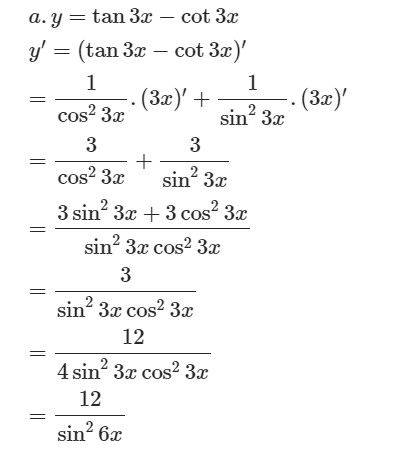Đạo Hàm tan3x: Công Thức, Ví Dụ và Ứng Dụng Chi Tiết

Việc tính đạo hàm của các hàm số lượng giác, đặc biệt là tan3x, là một kỹ năng quan trọng trong giải tích. Bài viết này sẽ cung cấp một cái nhìn sâu sắc về đạo hàm của tan3x, bao gồm công thức, ví dụ minh họa và ứng dụng thực tế.

Công thức đạo hàm của tan(u)

Trước khi đi vào tan3x, ta cần nắm vững công thức đạo hàm tổng quát của hàm tang:

(tan(u))' = u' / cos²(u) = u' * sec²(u)

Trong đó, u là một hàm số theo biến x.

Đạo hàm của tan3x

Áp dụng công thức trên với u = 3x, ta có:

(tan(3x))' = (3x)' / cos²(3x) = 3 / cos²(3x) = 3 * sec²(3x)

Vậy, đạo hàm của tan3x là 3sec²(3x).

Ví dụ minh họa

Ví dụ 1: Tính đạo hàm của hàm số y = tan3x + x²

Ta có:

y' = (tan3x)' + (x²)' = 3sec²(3x) + 2x

Ví dụ 2: Tính đạo hàm của hàm số y = (tan3x)²

Áp dụng quy tắc đạo hàm của hàm hợp:

y' = 2 * tan3x * (tan3x)' = 2 * tan3x * 3sec²(3x) = 6 * tan3x * sec²(3x)

Ứng dụng của đạo hàm tan3x

Đạo hàm của tan3x được sử dụng rộng rãi trong nhiều lĩnh vực của toán học và vật lý, bao gồm:

• Tìm cực trị của hàm số: Đạo hàm giúp xác định các điểm mà tại đó hàm số đạt giá trị lớn nhất hoặc nhỏ nhất.
• Xác định tính đơn điệu của hàm số: Dựa vào dấu của đạo hàm, ta có thể biết hàm số đồng biến hay nghịch biến trên một khoảng nhất định.
• Giải các bài toán liên quan đến chuyển động: Trong vật lý, đạo hàm của hàm vị trí theo thời gian cho ta vận tốc, và đạo hàm của vận tốc cho ta gia tốc. Các hàm lượng giác, bao gồm tan3x, thường xuất hiện trong mô tả dao động và sóng.

Mở rộng và nâng cao

Để hiểu sâu hơn về đạo hàm của tan3x, bạn có thể tìm hiểu thêm về:

• Các công thức lượng giác liên quan: Hiểu rõ các công thức lượng giác giúp đơn giản hóa biểu thức đạo hàm và giải quyết các bài toán phức tạp hơn.
• Đạo hàm cấp cao: Tính đạo hàm cấp hai, cấp ba của tan3x để phân tích kỹ hơn về tính chất của hàm số.
• Ứng dụng trong các bài toán thực tế: Tìm kiếm các ví dụ về ứng dụng của đạo hàm tan3x trong các lĩnh vực khác nhau để thấy rõ hơn tầm quan trọng của nó.

Tổng kết

Nắm vững công thức và cách tính đạo hàm của tan3x là một bước quan trọng để chinh phục các bài toán giải tích. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết để hiểu và áp dụng thành công đạo hàm của hàm số này.

Công thức đạo hàm của hàm số tan3x được trình bày rõ ràng, dễ hiểu, giúp người học dễ dàng áp dụng.

Bài giải chi tiết đạo hàm tan3x bằng hình ảnh, hỗ trợ người học tiếp thu kiến thức một cách trực quan.