Đạo hàm là một khái niệm quan trọng trong giải tích, giúp ta tìm hiểu tốc độ thay đổi của một hàm số. Trong bài viết này, chúng ta sẽ tập trung vào việc tìm hiểu đạo hàm của hàm số y = 3/x, một trường hợp thường gặp trong các bài toán.
Công thức đạo Hàm Của 3/x là gì? Làm thế nào để chứng minh công thức này? Ứng dụng của nó trong các bài toán thực tế ra sao? Hãy cùng khám phá.
Công Thức Đạo Hàm Của 3/x
Đạo hàm của hàm số y = 3/x, ký hiệu là y’, được tính như sau:
y’ = -3/x²
Chứng Minh Công Thức Đạo Hàm Của 3/x
Để chứng minh công thức trên, chúng ta có thể sử dụng định nghĩa đạo hàm hoặc quy tắc đạo hàm của hàm lũy thừa.
- Cách 1: Sử dụng định nghĩa đạo hàm
Định nghĩa đạo hàm của hàm số f(x) tại điểm x là:
f'(x) = lim (h->0) [f(x+h) – f(x)] / h
Áp dụng vào hàm số y = 3/x, ta có:
y’ = lim (h->0) [3/(x+h) – 3/x] / h
= lim (h->0) [3x – 3(x+h)] / [h x (x+h)]
= lim (h->0) [-3h] / [h x (x+h)]
= lim (h->0) -3 / [x * (x+h)]
= -3 / x²
- Cách 2: Sử dụng quy tắc đạo hàm của hàm lũy thừa
Ta có thể viết lại hàm số y = 3/x thành y = 3x⁻¹. Áp dụng quy tắc đạo hàm của hàm lũy thừa (d/dx (xⁿ) = n*xⁿ⁻¹), ta được:
y’ = 3 (-1) x⁻²
= -3x⁻²
= -3/x²
Cả hai cách đều cho ra kết quả giống nhau, chứng minh rằng đạo hàm của 3/x là -3/x².
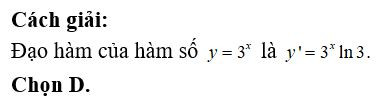
Công thức đạo hàm của y=3/x được minh họa bằng hình ảnh, cho thấy y’ = -3/x^2.
Ví Dụ Minh Họa
Giả sử chúng ta cần tìm đạo hàm của hàm số y = 3/x tại điểm x = 2. Áp dụng công thức vừa chứng minh, ta có:
y'(2) = -3 / 2² = -3/4
Vậy, đạo hàm của hàm số y = 3/x tại điểm x = 2 là -3/4. Điều này có nghĩa là tại điểm x = 2, hàm số đang giảm với tốc độ 3/4.
Ứng Dụng Của Đạo Hàm 3/x
Đạo hàm của 3/x và các hàm số tương tự có nhiều ứng dụng trong các lĩnh vực khác nhau:
- Vật lý: Tính vận tốc và gia tốc trong chuyển động. Ví dụ, nếu quãng đường đi được của một vật thể được biểu diễn bởi hàm số s(t) = 3/t (trong đó t là thời gian), thì vận tốc của vật thể tại thời điểm t sẽ là s'(t) = -3/t².
- Kinh tế: Phân tích sự thay đổi của chi phí, doanh thu, và lợi nhuận. Ví dụ, nếu chi phí trung bình để sản xuất một sản phẩm là C(x) = 3/x (trong đó x là số lượng sản phẩm), thì sự thay đổi của chi phí trung bình khi tăng sản lượng sẽ là C'(x) = -3/x².
- Toán học: Tìm cực trị của hàm số, giải các bài toán liên quan đến tiếp tuyến và pháp tuyến của đồ thị hàm số.
Bài Tập Vận Dụng
- Tìm đạo hàm của hàm số y = 6/x.
- Tìm phương trình tiếp tuyến của đồ thị hàm số y = 3/x tại điểm có hoành độ x = 1.
- Một vật thể chuyển động với quãng đường s(t) = 3/t. Tìm vận tốc của vật thể tại thời điểm t = 3.
Kết Luận
Hiểu rõ về đạo hàm của 3/x không chỉ giúp bạn giải quyết các bài toán trong sách giáo khoa mà còn mở ra cánh cửa để khám phá nhiều ứng dụng thực tế trong các lĩnh vực khác nhau. Việc nắm vững công thức và cách chứng minh sẽ giúp bạn tự tin hơn trong việc giải quyết các bài toán phức tạp hơn liên quan đến đạo hàm. Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và sâu sắc về đạo hàm của hàm số 3/x.
