Đạo hàm là một khái niệm quan trọng trong giải tích, giúp ta tìm hiểu tốc độ biến thiên của một hàm số. Trong bài viết này, chúng ta sẽ tập trung vào việc tìm hiểu về đạo hàm của hàm số cos² 2x, một dạng bài tập thường gặp trong chương trình Toán học phổ thông và cao cấp. Chúng ta sẽ đi sâu vào công thức, cách tính và các bài tập vận dụng để nắm vững kiến thức này.
Công Thức Đạo Hàm Lượng Giác Cơ Bản
Để tính đạo hàm cos² 2x, chúng ta cần nắm vững các công thức đạo hàm lượng giác cơ bản:
- (sinx)’ = cosx
- (cosx)’ = -sinx
- (tanx)’ = 1/cos²x
- (cotx)’ = -1/sin²x
Ngoài ra, chúng ta cần nhớ quy tắc đạo hàm của hàm hợp: (f(u))’ = f'(u) * u’
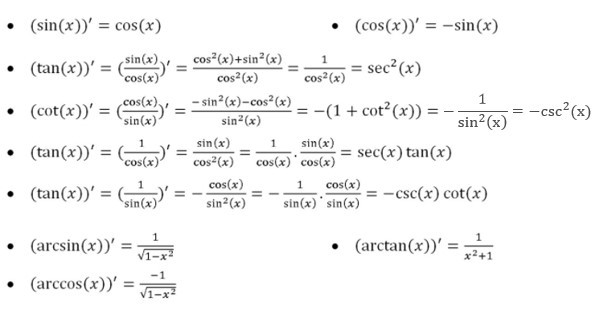Bảng công thức đạo hàm lượng giác cơ bản và đạo hàm lượng giác ngược để tham khảo và học thuộc
Cách Tính Đạo Hàm cos² 2x
Để tính đạo hàm cos² 2x, ta áp dụng quy tắc đạo hàm của hàm hợp và công thức đạo hàm của cosx:
- Đặt u = cos 2x. Khi đó, hàm số trở thành y = u².
- Tính đạo hàm của u theo x: u’ = (cos 2x)’ = -2sin 2x (áp dụng công thức (cos(ax))’ = -a*sin(ax)).
- Tính đạo hàm của y theo u: y’ = (u²)’ = 2u.
- Áp dụng quy tắc hàm hợp: (cos² 2x)’ = y’ u’ = 2u (-2sin 2x) = 2(cos 2x) * (-2sin 2x) = -4cos 2x sin 2x.
- Sử dụng công thức lượng giác: -4cos 2x sin 2x = -2(2sin 2x cos 2x) = -2sin 4x (vì 2sin a cos a = sin 2a).
Vậy, đạo hàm của cos² 2x là -2sin 4x.
Ví Dụ Minh Họa
Ví dụ 1: Tính đạo hàm của hàm số y = cos² 2x + x².
Áp dụng quy tắc đạo hàm tổng: y’ = (cos² 2x)’ + (x²)’ = -2sin 4x + 2x.
Ví dụ 2: Tính đạo hàm của hàm số y = sinx * cos² 2x.
Áp dụng quy tắc đạo hàm tích: y’ = (sinx)’ cos² 2x + sinx (cos² 2x)’ = cosx cos² 2x + sinx (-2sin 4x) = cosx cos² 2x – 2sinx sin 4x.
Bài Tập Vận Dụng
Để củng cố kiến thức, chúng ta cùng giải một số bài tập vận dụng sau:
Bài 1: Tính đạo hàm của hàm số y = (cos² 2x) / x.
Hướng dẫn:
Áp dụng quy tắc đạo hàm thương:
y’ = [(cos² 2x)’ x – cos² 2x (x)’] / x² = [(-2sin 4x) x – cos² 2x 1] / x² = (-2xsin 4x – cos² 2x) / x².
Bài 2: Cho hàm số f(x) = cos² 2x. Tính f'(π/4).
Hướng dẫn:
Đầu tiên, tính đạo hàm f'(x) = -2sin 4x.
Sau đó, thay x = π/4 vào f'(x): f'(π/4) = -2sin (4 * π/4) = -2sin π = 0.
Bài 3: Tìm cực trị của hàm số y = cos² 2x trên đoạn [0, π/2].
Hướng dẫn:
- Tính đạo hàm y’ = -2sin 4x.
- Giải phương trình y’ = 0, ta được -2sin 4x = 0 => sin 4x = 0 => 4x = kπ => x = kπ/4, với k là số nguyên.
- Xét các giá trị x thuộc đoạn [0, π/2]: x = 0, x = π/4, x = π/2.
- Tính giá trị của hàm số tại các điểm này và hai đầu mút của đoạn:
- y(0) = cos²(0) = 1
- y(π/4) = cos²(π/2) = 0
- y(π/2) = cos²(π) = 1
Vậy, hàm số đạt cực đại tại x = 0 và x = π/2 với giá trị bằng 1, và đạt cực tiểu tại x = π/4 với giá trị bằng 0.
Việc nắm vững công thức và cách tính đạo hàm cos² 2x không chỉ giúp bạn giải quyết các bài tập trong chương trình học, mà còn là nền tảng quan trọng để tiếp cận các khái niệm toán học cao cấp hơn. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và cần thiết. Hãy luyện tập thường xuyên để thành thạo kỹ năng này nhé!
