1. Dao Động Điều Hòa Là Gì?
Dao động là sự chuyển động qua lại của một vật quanh một vị trí cân bằng. Trong các loại dao động, Dao động điều Hòa đóng vai trò quan trọng, đặc biệt trong lĩnh vực vật lý.
Dao động điều hòa là một loại dao động tuần hoàn đặc biệt, trong đó li độ của vật dao động biến thiên theo thời gian theo quy luật hàm sin hoặc cosin. Nói cách khác, nó là hình chiếu của một chuyển động tròn đều lên một đường thẳng.
Ví dụ thực tế về dao động điều hòa:
- Chuyển động của con lắc lò xo (trong điều kiện lý tưởng, bỏ qua ma sát).
- Sự rung động của một sợi dây đàn guitar sau khi gảy.
- Chuyển động của một điểm trên mặt nước khi có sóng (nếu sóng có dạng sin).
2. Phương Trình Dao Động Điều Hòa
Phương trình mô tả dao động điều hòa có dạng:
x(t) = Acos(ωt + φ)
Trong đó:
- x(t): Li độ của vật tại thời điểm t (khoảng cách từ vật đến vị trí cân bằng).
- A: Biên độ dao động (giá trị cực đại của li độ).
- ω: Tần số góc (đo bằng rad/s, xác định tốc độ dao động).
- t: Thời gian (đo bằng giây).
- φ: Pha ban đầu (đo bằng radian, xác định trạng thái dao động tại thời điểm ban đầu).
, trong đó x là li độ, A là biên độ, omega là tần số góc, t là thời gian và phi là pha ban đầu.
3. Các Đại Lượng Đặc Trưng của Dao Động Điều Hòa
- Biên độ (A): Là độ lệch lớn nhất của vật so với vị trí cân bằng. Đơn vị thường là mét (m) hoặc centimet (cm).
- Chu kỳ (T): Là khoảng thời gian để vật thực hiện một dao động toàn phần. Đơn vị là giây (s). Công thức liên hệ với tần số góc: T = 2π/ω
- Tần số (f): Là số dao động toàn phần mà vật thực hiện trong một giây. Đơn vị là Hertz (Hz). Công thức liên hệ với chu kỳ: f = 1/T
- Tần số góc (ω): Đặc trưng cho tốc độ biến thiên của pha dao động. Đơn vị là radian trên giây (rad/s). Công thức liên hệ với tần số: ω = 2πf
- Pha dao động (ωt + φ): Xác định trạng thái dao động của vật tại thời điểm t. Đơn vị là radian (rad).
- Pha ban đầu (φ): Xác định trạng thái dao động của vật tại thời điểm t = 0. Đơn vị là radian (rad).
4. Vận Tốc và Gia Tốc Trong Dao Động Điều Hòa
Vận tốc và gia tốc của vật dao động điều hòa cũng biến thiên điều hòa theo thời gian.
- Vận tốc (v): Là đạo hàm của li độ theo thời gian:
v(t) = x'(t) = -Aωsin(ωt + φ)
Vận tốc đạt giá trị cực đại (vmax = Aω) khi vật đi qua vị trí cân bằng và bằng 0 ở vị trí biên. - Gia tốc (a): Là đạo hàm của vận tốc theo thời gian:
a(t) = v'(t) = -Aω²cos(ωt + φ) = -ω²x(t)
Gia tốc đạt giá trị cực đại (amax = Aω²) ở vị trí biên và bằng 0 ở vị trí cân bằng. Gia tốc luôn hướng về vị trí cân bằng.
%20%3D%20-A%5Comega%20sin(%5Comega%20t%20%2B%20%5Cvarphi)%2C%20a(t)%20%3D%20-A%5Comega%5E2%20cos(%5Comega%20t%20%2B%20%5Cvarphi)), thể hiện mối liên hệ giữa vận tốc, gia tốc, biên độ và tần số góc.
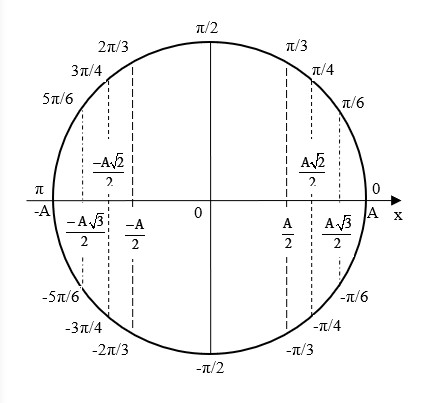
5. Mối Liên Hệ Giữa Dao Động Điều Hòa và Chuyển Động Tròn Đều
Dao động điều hòa có thể được xem là hình chiếu của một chuyển động tròn đều lên một đường kính của đường tròn đó. Tức là, nếu một chất điểm chuyển động tròn đều, hình chiếu của nó lên một trục tọa độ sẽ dao động điều hòa.
, minh họa cách dao động điều hòa có thể được biểu diễn bằng hình chiếu của chuyển động tròn đều. Alt: Dao động điều hòa và chuyển động tròn đều: hình chiếu của chuyển động tròn đều xuống trục tạo thành dao động điều hòa.
Mối liên hệ này giúp chúng ta dễ dàng hình dung và giải các bài toán liên quan đến dao động điều hòa bằng cách sử dụng các kiến thức về chuyển động tròn đều.
6. Năng Lượng Trong Dao Động Điều Hòa
Trong dao động điều hòa, năng lượng của hệ được bảo toàn và liên tục chuyển đổi giữa động năng và thế năng.
- Động năng (KE): KE = (1/2)mv² = (1/2)mA²ω²sin²(ωt + φ)
- Thế năng (PE): PE = (1/2)kx² = (1/2)mA²ω²cos²(ωt + φ) (với k là độ cứng của lò xo trong hệ con lắc lò xo)
- Cơ năng (E): E = KE + PE = (1/2)mA²ω² = const. Cơ năng của dao động điều hòa tỉ lệ với bình phương biên độ và bình phương tần số góc.
7. Các Dạng Bài Tập Về Dao Động Điều Hòa
Các bài tập về dao động điều hòa rất đa dạng, bao gồm:
- Xác định các đại lượng đặc trưng (A, T, f, ω, φ) từ phương trình dao động hoặc từ các dữ kiện bài toán.
- Viết phương trình dao động dựa trên các điều kiện ban đầu (li độ, vận tốc tại thời điểm t = 0).
- Tính vận tốc, gia tốc, động năng, thế năng tại một thời điểm hoặc vị trí nhất định.
- Tìm quãng đường, vận tốc trung bình, tốc độ trung bình trong một khoảng thời gian.
- Các bài toán liên quan đến con lắc lò xo, con lắc đơn.
, mô tả đồ thị hình sin của dao động điều hòa khi pha ban đầu bằng 0. Alt: Đồ thị dao động điều hòa: đồ thị li độ theo thời gian là một đường hình sin khi pha ban đầu bằng 0.
8. Ứng Dụng Của Dao Động Điều Hòa
Dao động điều hòa có rất nhiều ứng dụng trong thực tế:
- Đồng hồ: Sử dụng dao động của con lắc hoặc tinh thể thạch anh để đo thời gian.
- Âm nhạc: Sự rung động của dây đàn, màng loa tạo ra âm thanh.
- Điện tử: Mạch dao động trong các thiết bị điện tử (radio, tivi, điện thoại).
- Xây dựng: Nghiên cứu dao động của các công trình để đảm bảo an toàn.
- Y học: Sử dụng siêu âm (dao động cơ học tần số cao) để chẩn đoán và điều trị bệnh.
9. Tổng Kết
Dao động điều hòa là một khái niệm quan trọng trong vật lý, có nhiều ứng dụng trong khoa học và kỹ thuật. Việc nắm vững lý thuyết và các dạng bài tập liên quan sẽ giúp học sinh hiểu sâu sắc hơn về thế giới xung quanh và chuẩn bị tốt cho các kỳ thi.