Góc nội tiếp và Cung Bị Chắn là những khái niệm quan trọng trong hình học phẳng, đặc biệt là khi nghiên cứu về đường tròn. Hiểu rõ về chúng giúp giải quyết nhiều bài toán liên quan đến chứng minh và tính toán.
Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó. Cung nằm bên trong góc nội tiếp được gọi là cung bị chắn.
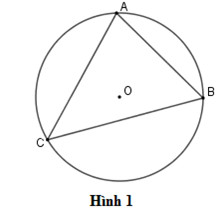Góc nội tiếp ACB chắn cung AB trong đường tròn
Hình ảnh minh họa góc nội tiếp ACB, với đỉnh C nằm trên đường tròn và hai cạnh CA, CB là các dây cung, chắn cung AB.
Định lý về góc nội tiếp: Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn. Ví dụ, nếu cung AB có số đo là 80 độ, thì góc nội tiếp chắn cung AB sẽ có số đo là 40 độ.
Hệ quả quan trọng:
- Các góc nội tiếp bằng nhau chắn các cung bằng nhau: Nếu hai góc nội tiếp có số đo bằng nhau thì hai cung mà chúng chắn cũng có độ dài bằng nhau.
- Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau: Hai góc nội tiếp cùng nhìn một cung sẽ có số đo bằng nhau. Điều này rất hữu ích trong việc chứng minh các góc bằng nhau trong các bài toán hình học.
- Góc nội tiếp (nhỏ hơn hoặc bằng 90°) có số đo bằng nửa số đo góc ở tâm cùng chắn một cung: Mối liên hệ này giúp liên kết giữa góc ở tâm và góc nội tiếp, mở rộng khả năng giải quyết bài toán.
- Góc nội tiếp chắn nửa đường tròn là góc vuông: Đây là một trường hợp đặc biệt và rất quan trọng. Nếu một góc nội tiếp chắn đường kính của đường tròn, góc đó sẽ là góc vuông.
Ứng dụng giải toán:
-
Chứng minh tam giác đồng dạng, hệ thức về cạnh, hai góc bằng nhau, các đoạn thẳng bằng nhau: Sử dụng hệ quả của định lý góc nội tiếp để suy ra các góc bằng nhau, từ đó áp dụng các tiêu chí đồng dạng của tam giác. Ví dụ, nếu hai góc nội tiếp cùng chắn một cung, chúng bằng nhau và có thể được sử dụng để chứng minh hai tam giác đồng dạng.
-
Chứng minh hai đường thẳng vuông góc, song song. Tính độ dài, diện tích: Ứng dụng hệ quả về góc nội tiếp chắn nửa đường tròn là góc vuông để chứng minh hai đường thẳng vuông góc. Sử dụng các tính chất của góc nội tiếp để suy ra các góc bằng nhau, từ đó chứng minh các đường thẳng song song. Việc tính toán độ dài và diện tích thường liên quan đến việc xác định các góc và cạnh thông qua các định lý và hệ quả liên quan đến cung bị chắn.