Trong giải tích, việc xác định Cực đại Của Hàm Số là một trong những nhiệm vụ quan trọng, giúp ta hiểu rõ hơn về sự biến thiên và đặc điểm của hàm số. Bài viết này sẽ cung cấp một cái nhìn toàn diện về cực đại của hàm số, từ định nghĩa đến các phương pháp tìm kiếm và ứng dụng.
1. Định Nghĩa Cực Đại của Hàm Số
Điểm cực đại của hàm số là điểm mà tại đó hàm số đạt giá trị lớn nhất trong một lân cận của điểm đó. Nói cách khác, nếu xét một khoảng (a; b) chứa điểm x₀ và f(x) ≤ f(x₀) với mọi x thuộc (a; b), thì x₀ là điểm cực đại của hàm số f(x), và f(x₀) là giá trị cực đại của hàm số.
Lưu ý rằng giá trị cực đại không nhất thiết là giá trị lớn nhất của hàm số trên toàn bộ tập xác định. Nó chỉ là giá trị lớn nhất trong một vùng lân cận.
2. Các Định Lý và Dấu Hiệu Nhận Biết Điểm Cực Đại
Để xác định điểm cực đại của hàm số, ta có thể sử dụng các định lý và quy tắc sau:
2.1. Định Lý 1 (Điều kiện cần):
Nếu hàm số f(x) đạt cực đại tại điểm x₀ và có đạo hàm tại điểm đó, thì f'(x₀) = 0.
Lưu ý: Định lý này chỉ là điều kiện cần, nghĩa là nếu f'(x₀) = 0, x₀ có thể là điểm cực đại, cực tiểu hoặc không phải là điểm cực trị.
2.2. Định Lý 2 (Điều kiện đủ – Quy tắc 1):
Nếu f'(x) đổi dấu từ dương sang âm khi x đi qua điểm x₀ (theo chiều tăng), thì hàm số đạt cực đại tại điểm x₀.
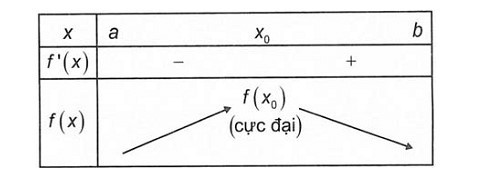Đồ thị hàm số đạt cực đại khi f'(x) đổi dấu từ dương sang âm
Alt: Đồ thị minh họa hàm số đạt cực đại tại x0 khi đạo hàm f'(x) đổi dấu từ dương sang âm, thể hiện xu hướng tăng rồi giảm.
2.3. Định Lý 3 (Điều kiện đủ – Quy tắc 2):
Giả sử f'(x₀) = 0 và f”(x₀) < 0, thì hàm số f(x) đạt cực đại tại điểm x₀.
Lưu ý: Nếu f”(x₀) = 0, ta cần sử dụng các phương pháp khác để xác định tính cực trị của hàm số tại x₀ (ví dụ: xét dấu của f'(x) xung quanh x₀).
3. Các Bước Tìm Điểm Cực Đại của Hàm Số
Dưới đây là quy trình chi tiết để tìm điểm cực đại của hàm số:
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Tính đạo hàm cấp nhất f'(x) của hàm số.
Bước 3: Giải phương trình f'(x) = 0 để tìm các điểm tới hạn xᵢ.
Bước 4:
- Cách 1 (Sử dụng định lý 2): Lập bảng biến thiên của f'(x) và xét dấu của f'(x) xung quanh các điểm tới hạn xᵢ. Nếu f'(x) đổi dấu từ dương sang âm khi x đi qua xᵢ, thì xᵢ là điểm cực đại.
- Cách 2 (Sử dụng định lý 3): Tính đạo hàm cấp hai f”(x) của hàm số. Thay các điểm tới hạn xᵢ vào f”(x). Nếu f”(xᵢ) < 0, thì xᵢ là điểm cực đại.
Bước 5: Kết luận các điểm cực đại và giá trị cực đại tương ứng của hàm số.
4. Ví Dụ Minh Họa
Ví dụ 1: Tìm cực đại của hàm số y = -x² + 4x – 3
- Bước 1: Tập xác định D = R.
- Bước 2: y’ = -2x + 4
- Bước 3: y’ = 0 <=> -2x + 4 = 0 <=> x = 2
- Bước 4: y” = -2 < 0. Vậy x = 2 là điểm cực đại.
- Bước 5: Giá trị cực đại là y(2) = -2² + 4*2 – 3 = 1.
Ví dụ 2: Tìm cực đại của hàm số y = x³ – 3x
- Bước 1: Tập xác định D = R.
- Bước 2: y’ = 3x² – 3
- Bước 3: y’ = 0 <=> 3x² – 3 = 0 <=> x = ±1
- Bước 4: y” = 6x.
- y”(-1) = -6 < 0. Vậy x = -1 là điểm cực đại.
- y”(1) = 6 > 0. Vậy x = 1 là điểm cực tiểu.
- Bước 5: Giá trị cực đại là y(-1) = (-1)³ – 3*(-1) = 2.
5. Ứng Dụng của Cực Đại Hàm Số
Việc tìm cực đại của hàm số có rất nhiều ứng dụng thực tế, ví dụ:
- Tối ưu hóa: Tìm giá trị lớn nhất của một hàm mục tiêu trong một bài toán tối ưu.
- Kinh tế: Xác định mức sản lượng tối ưu để đạt lợi nhuận cao nhất.
- Vật lý: Tìm vị trí mà tại đó thế năng đạt giá trị lớn nhất.
6. Lưu Ý Quan Trọng
- Khi giải các bài toán tìm cực đại của hàm số, cần chú ý đến tập xác định của hàm số.
- Cần phân biệt rõ điểm cực đại và giá trị cực đại. Điểm cực đại là giá trị x, còn giá trị cực đại là giá trị y tương ứng.
- Không phải hàm số nào cũng có cực đại.
- Khi sử dụng đạo hàm cấp hai để xác định cực trị, nếu f”(x₀) = 0, cần sử dụng các phương pháp khác để xét.
7. Kết Luận
Hiểu rõ về cực đại của hàm số là một phần quan trọng trong chương trình toán học phổ thông và đại học. Nắm vững lý thuyết và các phương pháp tìm kiếm sẽ giúp bạn giải quyết các bài toán liên quan một cách hiệu quả và ứng dụng kiến thức này vào thực tế.
