Giá trị của Cos45 bằng 1/√2, một con số quan trọng trong lượng giác.
Trong lượng giác, sin, cos và tan là ba tỉ số cơ bản. Giá trị của các tỉ số lượng giác này phụ thuộc vào các cạnh của tam giác vuông. Cos của một góc bằng tỉ số giữa cạnh kề và cạnh huyền. Công thức tổng quát là: Cos θ = Cạnh Kề / Cạnh Huyền
Giá Trị Chính Xác của Cos45
Giá trị chính xác của cos45 độ là 1/√2 (dạng căn thức), cũng bằng giá trị của sin45 độ. Đây là một số vô tỉ, xấp xỉ bằng 0.7071067812… ở dạng thập phân. Giá trị gần đúng của cos45 là 0.7071 hoặc có thể viết là √2/2.
| Cos 45° = 1/√2 = √2/2 |
|---|
Vì vậy, 0.7071 hoặc 1/√2 là giá trị của một hàm lượng giác hay tỉ số lượng giác của góc đặc biệt (45 độ).
Chứng Minh Giá Trị Cos45
Giả sử chúng ta có một tam giác vuông, trong đó hai góc còn lại bằng 45 độ. Khi đó, nếu các góc của một tam giác vuông là 45 độ, thì các cạnh kề bằng nhau về độ dài.
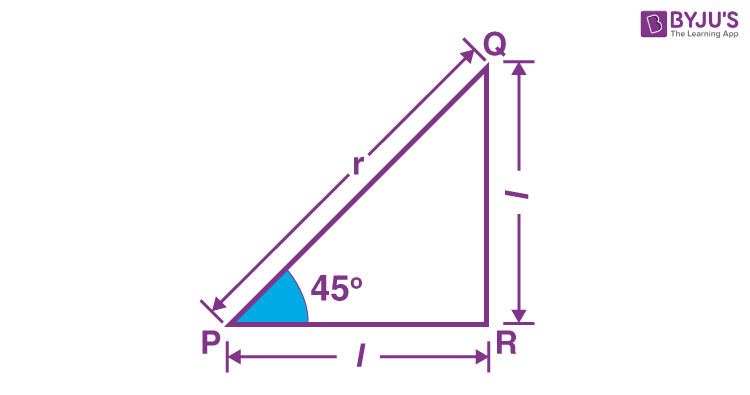Tam giác vuông cân với góc 45 độ để chứng minh cos45 bằng 1 trên căn 2
Giả sử độ dài của các cạnh kề bằng ‘l’ và cạnh huyền là ‘r’.
Theo định lý Pythagoras, ta có: Cạnh huyền² = Cạnh góc vuông 1² + Cạnh góc vuông 2²
PQ² = PR² + QR²
⇒ r² = l² + l²
⇒ r = √2 l
⇒ l/r = 1/√2
Vậy, Độ dài cạnh kề / Cạnh huyền = 1/√2
Do đó, ta có thể nói: Cos 45° = 1/√2
Vậy, chứng minh xong.
Mối Liên Hệ Giữa Cos45 và Sin45
Chúng ta cũng có thể chứng minh giá trị của cos45° bằng cách sử dụng phương pháp lượng giác.
Như chúng ta đã biết, sin 45° = 1/√2
Ngoài ra, theo các hằng đẳng thức lượng giác, chúng ta biết rằng:
Sin² x + cos² x = 1
Hoặc Cos² x = 1 – sin² x
Đặt x = 45°
Cos² 45° = 1 – sin² 45°
Thay giá trị của sin 45° vào phương trình trên.
Cos² 45° = 1 – (1/√2)²
Cos² 45° = 1 – ½
Cos 45° = √1/2 = 1/√2
Vậy, ta đã tìm ra giá trị của cos 45°.
Bảng Giá Trị Cos
| Góc | Giá trị Cos |
|---|---|
| Cos 0° | 1 |
| Cos 30° (Cos π/6) | √3/2 |
| Cos 45° (Cos π/4) | 1/√2 |
| Cos 60° (Cos π/3) | 1/2 |
| Cos 90° (Cos π/2) | 0 |
| Cos 120° (Cos 2π/3) | -1/2 |
| Cos 150° (Cos 5π/6) | -√3/2 |
| Cos 180° (Cos π) | -1 |
| Cos 270° (Cos 3π/2) | 0 |
| Cos 360° (Cos 2π) | 1 |
Ví Dụ Minh Họa
Câu hỏi 1: Tìm giá trị của cos 45° + sin 30°
Giải: Cho cos 45° + sin 30°
cos 45° + sin 30° = 1/√2 + ½ = (√2+1)/2
Câu hỏi 2: Tính: 2 sin 60° – 4 cos 45°
Giải: Cho 2 sin 60° – 4 cos 45°
Vì sin 60° = √3/2 và cos 45° = 1/√2
Do đó: ⇒ 2 (√3/2) – 4 (1/√2)
⇒ √3 – 2√2
Câu hỏi 3: Tìm Cos 45 + Cos 90.
Giải: Cos 45° = 1/√2
Cos 90° = 0
Do đó, Cos 45° + cos 90° = 1/√2 + 0 = 1/√2
Bài Tập Luyện Tập
- Tính 2 cos 45° + cos 0°
- Tìm giá trị của sin 60° – cos 45°.
- Tan 45° – cos 45° = ?
- Cos 45° – ½ (Cot 45°) = ?
Câu Hỏi Thường Gặp Về Cos45
Câu hỏi 1: Giá trị chính xác của cos 45 độ là bao nhiêu?
Giá trị chính xác của cos 45 độ là 1/√2 hoặc √2/2.
Câu hỏi 2: Cos 45 và sin 45 có giống nhau không?
Có, giá trị của cos 45 và sin 45 là giống nhau, đều bằng 1/√2.
Câu hỏi 3: Giá trị của cos 90 là bao nhiêu?
Giá trị của cos 90 bằng 0.
Câu hỏi 4: Tổng của cos 45 và sin 45 là bao nhiêu?
Cos 45 + Sin 45 = 1/√2 + 1/√2 = 2/√2 = √2
Câu hỏi 5: Làm thế nào để tính giá trị của cos 45?
Chúng ta có thể sử dụng định lý Pythagoras để tìm giá trị của cos 45. Vì, đối với một góc vuông, nếu các góc kề là 45 độ, thì cạnh kề và cạnh đối diện sẽ bằng nhau. Do đó, chúng ta có thể tìm giá trị của cos 45 bằng 1/√2.
