Bài viết này tổng hợp và giới thiệu các Công Thức Tính Thể Tích Khối Tứ Diện, bao gồm cả các trường hợp đặc biệt và công thức tổng quát, giúp bạn giải quyết nhanh các bài toán liên quan.
Công thức tổng quát: Cho khối tứ diện $ABCD$ với $BC=a, CA=b, AB=c, AD=d, BD=e, CD=f$, thể tích được tính như sau:
$V=dfrac{1}{12}sqrt{M+N+P-Q}$
Trong đó:
$M={{a}^{2}}{{d}^{2}}({{b}^{2}}+{{e}^{2}}+{{c}^{2}}+{{f}^{2}}-{{a}^{2}}-{{d}^{2}})$
$N={{b}^{2}}{{e}^{2}}({{a}^{2}}+{{d}^{2}}+{{c}^{2}}+{{f}^{2}}-{{b}^{2}}-{{e}^{2}})$
$P={{c}^{2}}{{f}^{2}}({{a}^{2}}+{{d}^{2}}+{{b}^{2}}+{{e}^{2}}-{{c}^{2}}-{{f}^{2}})$
$Q={{(abc)}^{2}}+{{(aef)}^{2}}+{{(bdf)}^{2}}+{{(cde)}^{2}}$
Công thức này cho phép tính thể tích khi biết độ dài tất cả 6 cạnh của tứ diện.
1. Khối Tứ Diện Đều
Với khối tứ diện đều cạnh $a$, thể tích được tính đơn giản:
$V=dfrac{{{a}^{3}}sqrt{2}}{12}$
Ví dụ: Cho tứ diện đều có chiều cao $h$. Thể tích của khối tứ diện là bao nhiêu?
Giải:
Ta có: $h = asqrt{dfrac{2}{3}} Rightarrow a = hsqrt{dfrac{3}{2}}$
$V = dfrac{a^3sqrt{2}}{12} = dfrac{(hsqrt{frac{3}{2}})^3sqrt{2}}{12} = dfrac{h^3sqrt{3}}{8}$
2. Khối Tứ Diện Vuông
Trong tứ diện $ABCD$, nếu $AB, AC, AD$ đôi một vuông góc và $AB=a, AC=b, AD=c$, thể tích là:
$V=dfrac{1}{6}abc$
3. Khối Tứ Diện Gần Đều
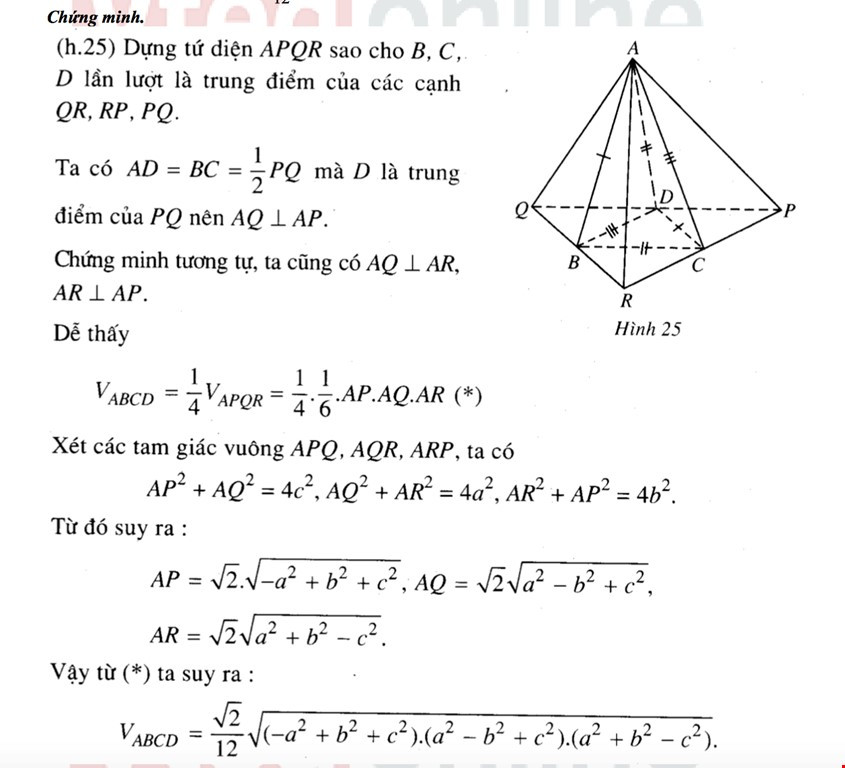
Tứ diện $ABCD$ có $AB=CD=a, BC=AD=b, AC=BD=c$, thể tích được tính bằng công thức:
$V=dfrac{sqrt{2}}{12}.sqrt{({{a}^{2}}+{{b}^{2}}-{{c}^{2}})({{b}^{2}}+{{c}^{2}}-{{a}^{2}})({{a}^{2}}+{{c}^{2}}-{{b}^{2}})}$
Ví dụ: Cho khối tứ diện $ABCD$ có $AB=CD=8, AD=BC=5, AC=BD=7$. Tính thể tích khối tứ diện.
Giải:
Áp dụng công thức trên:
$V = dfrac{sqrt{2}}{12}sqrt{(8^2 + 5^2 – 7^2)(5^2 + 7^2 – 8^2)(7^2 + 8^2 – 5^2)} = dfrac{20sqrt{11}}{3}$
4. Khối Tứ Diện Với Khoảng Cách Và Góc Giữa Cặp Cạnh Đối Diện
Cho tứ diện $ABCD$ có $AD=a, BC=b$, khoảng cách giữa $AD$ và $BC$ là $d$, góc giữa $AD$ và $BC$ là $alpha$, ta có:
$V=dfrac{1}{6}abdsin alpha$
5. Khối Tứ Diện Với Diện Tích Hai Mặt Kề Nhau
Nếu biết diện tích hai mặt và góc giữa chúng, công thức tính thể tích trở nên hữu ích.
6. Mở Rộng Cho Khối Chóp
Khối chóp $S.A_1A_2…A_n$ có thể tích:
$V=dfrac{2{{S}_{S{{A}_{1}}{{A}_{2}}}}.{{S}_{{{A}_{1}}{{A}_{2}}…{{A}_{n}}}}.sin left( (S{{A}_{1}}{{A}_{2}}),({{A}_{1}}{{A}_{2}}…{{A}_{n}}) right)}{3{{A}_{1}}{{A}_{2}}}$
7. Khối Tứ Diện Khi Biết Các Góc Tại Cùng Một Đỉnh
Cho khối chóp $S.ABC$ có $SA=a, SB=b, SC=c, widehat{BSC}=alpha, widehat{CSA}=beta, widehat{ASB}=gamma$. Thể tích được tính như sau:
$V=dfrac{abc}{6}sqrt{1+2cos alpha cos beta cos gamma -{{cos }^{2}}alpha -{{cos }^{2}}beta -{{cos }^{2}}gamma }$
Ví dụ: Cho hình chóp $S.ABC$ có $SA=a, SB=2a, SC=4a$ và $widehat{ASB}=widehat{BSC}=widehat{CSA}=60^circ$. Tính thể tích khối chóp $S.ABC$.
Giải:
$V=dfrac{1}{6}a cdot 2a cdot 4a sqrt{1 + 2cos 60^circ cos 60^circ cos 60^circ – cos^2 60^circ – cos^2 60^circ – cos^2 60^circ} = dfrac{2sqrt{2}a^3}{3}$
Bài viết này cung cấp một cái nhìn tổng quan và chi tiết về các công thức tính thể tích khối tứ diện, giúp bạn áp dụng linh hoạt vào giải quyết các bài toán hình học không gian.