Công Thức Tính Thể Tích Hình Lăng Trụ: Chi Tiết và Bài Tập Áp Dụng

1. Hình Lăng Trụ Là Gì?

Hình lăng trụ là một khối đa diện được giới hạn bởi hai mặt đáy là hai đa giác phẳng, bằng nhau và song song với nhau, và các mặt bên là các hình bình hành.

1.1. Hình Lăng Trụ Tam Giác Đều

Hình lăng trụ tam giác đều là hình lăng trụ đứng có hai mặt đáy là các tam giác đều.

1.2. Hình Lăng Trụ Tứ Giác Đều

Hình lăng trụ tứ giác đều là hình lăng trụ đứng có hai mặt đáy là các hình vuông. Hay còn gọi là hình hộp chữ nhật có đáy là hình vuông.

2. Các Dạng Hình Lăng Trụ Thường Gặp

• Lăng trụ đứng: Lăng trụ có các cạnh bên vuông góc với mặt đáy. Chiều dài cạnh bên chính là chiều cao của lăng trụ. Mặt bên của lăng trụ đứng là hình chữ nhật.
• Lăng trụ đều: Lăng trụ đứng có đáy là đa giác đều. Các mặt bên là các hình chữ nhật bằng nhau.
• Hình hộp: Lăng trụ có đáy là hình bình hành.
• Hình hộp đứng: Lăng trụ đứng có đáy là hình bình hành.
• Hình hộp chữ nhật: Hình hộp đứng có đáy là hình chữ nhật.
• Hình lập phương: Lăng trụ đứng có đáy là hình vuông và các mặt bên là hình vuông.

3. Công Thức Tính Thể Tích Hình Lăng Trụ

Công thức tổng quát:

Thể tích của hình lăng trụ bằng diện tích đáy nhân với chiều cao của lăng trụ.

V = B.h

Trong đó:

• V: Thể tích hình lăng trụ (đơn vị thể tích: m³, cm³, …)
• B: Diện tích mặt đáy (đơn vị diện tích: m², cm², …)
• h: Chiều cao của hình lăng trụ (khoảng cách giữa hai mặt đáy) (đơn vị độ dài: m, cm, …)

Ví dụ:

• Lăng trụ tam giác: Nếu đáy là tam giác có cạnh đáy a và chiều cao h_a, thì B = (1/2) a h_a.
• Lăng trụ tứ giác (hình hộp): Nếu đáy là hình chữ nhật có chiều dài l và chiều rộng w, thì B = l * w.
• Lăng trụ đều: Nếu đáy là đa giác đều có diện tích S, thì B = S.

4. Bài Tập Vận Dụng và Phương Pháp Giải

Bài 1: Cho hình lăng trụ đứng ABC.A′B′C′ có đáy ABC là tam giác đều cạnh a. Mặt phẳng (A’BC) tạo với đáy một góc 60°. Tính thể tích khối lăng trụ.

Giải:

1. Tính diện tích đáy: Vì ABC là tam giác đều cạnh a, diện tích đáy là S_ABC = (a²√3) / 4.
2. Xác định chiều cao: Gọi H là trung điểm BC. Ta có AH ⊥ BC và A’H ⊥ BC. Góc giữa (A’BC) và (ABC) là góc A’HA = 60°.
3. Tính AH: AH = (a√3) / 2.
4. Tính AA’: Trong tam giác vuông A’HA, ta có AA’ = AH tan(60°) = (a√3) / 2 √3 = (3a) / 2.
5. Tính thể tích: V = S_ABC AA’ = ((a²√3) / 4) ((3a) / 2) = (3a³√3) / 8.

Bài 2: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a, đường chéo của mặt bên ABB’A’ là AB’ = a√2. Tính thể tích của khối lăng trụ ABC.A’B’C’.

Giải:

1. Tính chiều cao: Tam giác ABB’ vuông tại A, có AB’ = a√2 và AB = a. Sử dụng định lý Pythagoras, ta có BB’ = √(AB’² – AB²) = √(2a² – a²) = a.
2. Tính diện tích đáy: Vì ABC là tam giác đều cạnh a, diện tích đáy là S_ABC = (a²√3) / 4.
3. Tính thể tích: V = S_ABC BB’ = ((a²√3) / 4) a = (a³√3) / 4.

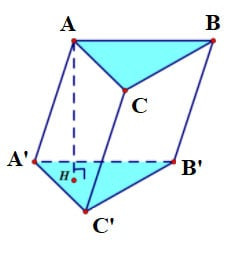
Bài 3: Cho lăng trụ xiên tam giác ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Hình chiếu của A’ xuống (ABC) là tâm O của đường tròn ngoại tiếp tam giác ABC, AA’ hợp với đáy (ABC) một góc 60 độ. Tính thể tích khối lăng trụ.

Giải:

1. Tính diện tích đáy: Vì ABC là tam giác đều cạnh a, diện tích đáy là S_ABC = (a²√3) / 4.
2. Tính AO: Vì O là tâm đường tròn ngoại tiếp tam giác đều ABC, AO = (2/3) * AH, với AH là đường cao của tam giác ABC. AH = (a√3) / 2, suy ra AO = (a√3) / 3.
3. Tính A’O: Tam giác A’AO vuông tại O, góc A’AO = 60°. Ta có A’O = AO tan(60°) = ((a√3) / 3) √3 = a.
4. Tính thể tích: V = S_ABC A’O = ((a²√3) / 4) a = (a³√3) / 4.

Bài 4: Cho hình hộp ABCD.A’B’C’D’ có đáy là hình chữ nhật với AB = √3, AD = √7. Hai mặt bên (ABB’A’) và (ADD’A’) tạo với đáy lần lượt các góc 45° và 60°. Tính thể tích khối hộp nếu biết cạnh bên bằng 1.

Giải:

1. Tính diện tích đáy: Vì ABCD là hình chữ nhật, S_ABCD = AB AD = √3 √7 = √21.
2. Xác định hình chiếu: Gọi H là hình chiếu của A’ trên mặt phẳng (ABCD). Gọi M, N lần lượt là hình chiếu của H trên AB và AD. Khi đó góc giữa (ABB’A’) và (ABCD) là góc A’MA = 45°, góc giữa (ADD’A’) và (ABCD) là góc A’NA = 60°.
3. Tính AM, AN: Tam giác A’MA vuông tại M, A’M = A’A cos(45°) = 1 (√2 / 2) = √2 / 2. Tương tự, AN = A’A cos(60°) = 1 (1/2) = 1/2.
4. Tính HM, HN: Trong tam giác vuông A’HM, HM = A’M = √2 / 2. Trong tam giác vuông A’HN, HN = A’N = 1/2.
5. Tính AH: Ta có AH² = HM² + HN² = (√2 / 2)² + (1/2)² = 1/2 + 1/4 = 3/4. Vậy AH = √(3/4) = √3 / 2.
6. Tính thể tích: V = S_ABCD AH = √21 (√3 / 2) = (3√7) / 2.

Nắm vững công thức và luyện tập thường xuyên sẽ giúp bạn dễ dàng giải quyết các bài toán liên quan đến thể tích hình lăng trụ. Chúc bạn học tốt!