Đường chéo hình vuông là một khái niệm quan trọng trong hình học, xuất hiện nhiều trong các bài toán và ứng dụng thực tế. Bài viết này sẽ cung cấp kiến thức đầy đủ và chi tiết về Công Thức Tính đường Chéo Của Hình Vuông, đi kèm với ví dụ minh họa và mở rộng liên quan.
Đường Chéo Hình Vuông Là Gì?
Đường chéo của hình vuông là đoạn thẳng nối hai đỉnh đối diện của hình vuông đó. Mỗi hình vuông có hai đường chéo, và chúng có những tính chất đặc biệt.
Tính Chất Quan Trọng Của Đường Chéo Hình Vuông
- Độ dài bằng nhau: Hai đường chéo của hình vuông có độ dài bằng nhau.
- Vuông góc với nhau: Hai đường chéo của hình vuông cắt nhau tại trung điểm và vuông góc với nhau.
- Chia hình vuông thành hai tam giác vuông cân: Mỗi đường chéo chia hình vuông thành hai tam giác vuông cân bằng nhau.
Công Thức Tính Đường Chéo Của Hình Vuông
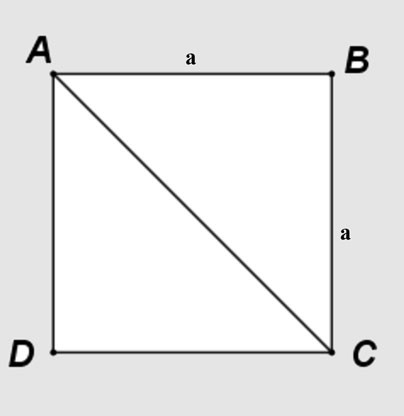
Giả sử hình vuông ABCD có cạnh là a. Đường chéo AC chia hình vuông thành hai tam giác vuông cân ABC và ADC. Để tính độ dài đường chéo AC, ta áp dụng định lý Pytago cho tam giác vuông ABC:
AC² = AB² + BC² = a² + a² = 2a²
Vậy, độ dài đường chéo AC của hình vuông là:
AC = a√2
Đây là công thức quan trọng cần ghi nhớ. Đường chéo hình vuông bằng cạnh nhân căn bậc hai của 2.
Ví Dụ Minh Họa
Ví dụ 1: Cho hình vuông có cạnh dài 5cm. Tính độ dài đường chéo của hình vuông đó.
Giải:
Áp dụng công thức, ta có:
Đường chéo = 5√2 cm ≈ 7.07 cm
Ví dụ 2: Một hình vuông có diện tích 16 cm². Tính độ dài đường chéo của hình vuông đó.
Giải:
Đầu tiên, ta tìm độ dài cạnh của hình vuông:
Diện tích hình vuông = a² = 16 cm²
=> a = √16 = 4 cm
Sau đó, áp dụng công thức tính đường chéo:
Đường chéo = 4√2 cm ≈ 5.66 cm
Ứng Dụng Thực Tế Của Công Thức Tính Đường Chéo Hình Vuông
Công thức này được ứng dụng rộng rãi trong nhiều lĩnh vực:
- Xây dựng: Tính toán kích thước các cấu trúc vuông, đảm bảo độ chính xác và cân đối.
- Thiết kế: Thiết kế nội thất, ngoại thất, và các vật dụng có hình dạng vuông.
- Cắt gọt: Cắt vật liệu thành hình vuông, đảm bảo các góc vuông và đường chéo chính xác.
- Toán học và Vật lý: Giải các bài toán liên quan đến hình học phẳng và không gian.
Mở Rộng: Liên Hệ Giữa Đường Chéo Hình Vuông và Đường Chéo Hình Chữ Nhật
Hình vuông là một trường hợp đặc biệt của hình chữ nhật, khi chiều dài và chiều rộng bằng nhau. Do đó, ta có thể xem xét công thức tính đường chéo hình chữ nhật như một phiên bản tổng quát hơn.
Công thức tính đường chéo hình chữ nhật:
Cho hình chữ nhật ABCD có chiều dài là a và chiều rộng là b. Áp dụng định lý Pytago, ta có:
AC² = AB² + BC² = a² + b²
=> AC = √(a² + b²)
Khi a = b, hình chữ nhật trở thành hình vuông, và công thức trở thành AC = √(a² + a²) = √(2a²) = a√2, trùng với công thức tính đường chéo hình vuông đã biết.
Bài Tập Vận Dụng
- Một hình vuông có chu vi là 20cm. Tính độ dài đường chéo của hình vuông đó.
- Một hình vuông được tạo thành từ việc cắt một hình tròn có bán kính 5cm. Tính độ dài đường chéo của hình vuông lớn nhất có thể cắt được.
- Cho hình vuông ABCD. Gọi M là trung điểm của cạnh AB. Tính độ dài đoạn thẳng CM, biết cạnh của hình vuông là 6cm. (Gợi ý: Sử dụng định lý Pytago).
Kết Luận
Nắm vững công thức tính đường chéo của hình vuông và các tính chất liên quan sẽ giúp bạn giải quyết các bài toán hình học một cách dễ dàng và chính xác hơn. Hy vọng bài viết này cung cấp cho bạn đầy đủ kiến thức cần thiết về chủ đề này.