Công Thức Tính Đường Cao Của Tam Giác: Chi Tiết và Dễ Hiểu

Đường cao là một yếu tố quan trọng trong hình học tam giác. Bài viết này sẽ cung cấp đầy đủ các công thức tính đường cao trong các loại tam giác khác nhau, kèm theo ví dụ minh họa dễ hiểu và tối ưu SEO cho người dùng Việt Nam.

Định Nghĩa Đường Cao Tam Giác

Đường cao của tam giác là đoạn thẳng kẻ từ một đỉnh của tam giác và vuông góc với cạnh đối diện (hoặc đường kéo dài của cạnh đối diện). Cạnh đối diện này được gọi là cạnh đáy tương ứng với đường cao đó.

Công Thức Tính Đường Cao Trong Tam Giác Thường

Để tính đường cao trong tam giác thường (tam giác không có các tính chất đặc biệt như vuông, cân, đều), chúng ta có thể sử dụng công thức Heron để tính diện tích, sau đó suy ra chiều cao.

Công thức Heron:

• Gọi a, b, c là độ dài ba cạnh của tam giác.
• Nửa chu vi p = (a + b + c) / 2
• Diện tích tam giác S = √[p(p-a)(p-b)(p-c)]

Sau khi có diện tích S, ta có thể tính đường cao h_a (đường cao ứng với cạnh a) theo công thức:

h_a = 2S / a

Alt: Công thức tính đường cao ha trong tam giác thường thông qua diện tích S và cạnh đáy a, sử dụng công thức Heron để tính S.

Ví dụ:

Cho tam giác ABC có AB = 4 cm, BC = 7 cm, AC = 5 cm. Tính đường cao AH kẻ từ A xuống BC.

• Nửa chu vi: p = (4 + 7 + 5) / 2 = 8 cm
• Diện tích: S = √[8(8-4)(8-7)(8-5)] = √(841*3) = √96 = 4√6 cm²
• Đường cao AH: AH = (2 * 4√6) / 7 = (8√6) / 7 cm

Công Thức Tính Đường Cao Trong Tam Giác Đều

Trong tam giác đều, ba cạnh bằng nhau và ba góc bằng 60 độ. Đường cao của tam giác đều cũng đồng thời là đường trung tuyến, đường trung trực và đường phân giác.

Nếu tam giác đều ABC có cạnh bằng a, thì đường cao h được tính theo công thức:

h = (a√3) / 2

Alt: Công thức tính đường cao h của tam giác đều với cạnh a, sử dụng căn bậc hai của 3.

Công Thức Tính Đường Cao Trong Tam Giác Vuông

Trong tam giác vuông, có một góc bằng 90 độ. Đường cao kẻ từ đỉnh góc vuông xuống cạnh huyền có thể được tính bằng nhiều cách, sử dụng các hệ thức lượng trong tam giác vuông.

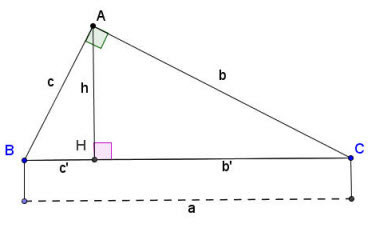
Cho tam giác ABC vuông tại A, AH là đường cao kẻ từ A xuống BC. Ta có các công thức sau:

1. Sử dụng hệ thức lượng: AH BC = AB AC => AH = (AB * AC) / BC
2. Sử dụng định lý Pythagoras: BC² = AB² + AC² (tính BC trước)
3. Các hệ thức liên quan đến hình chiếu:
   • AB² = BH * BC
   • AC² = CH * BC
   • AH² = BH * CH

Alt: Tam giác vuông ABC tại A với đường cao AH, minh họa các cạnh a, b, c và hình chiếu b’, c’ trên cạnh huyền để tính toán.

Ví dụ:

Cho tam giác ABC vuông tại A, AB = 15 cm, AC = 20 cm. Tính đường cao AH.

• BC² = 15² + 20² = 225 + 400 = 625 => BC = 25 cm
• AH = (15 * 20) / 25 = 12 cm

Alt: Bài toán tam giác vuông ABC với đường cao AH, yêu cầu tính độ dài các cạnh BC, AC, và AH khi biết AB và HC.

Công Thức Tính Đường Cao Trong Tam Giác Cân

Tam giác cân là tam giác có hai cạnh bằng nhau. Trong tam giác cân, đường cao kẻ từ đỉnh cân xuống cạnh đáy đồng thời là đường trung tuyến, đường trung trực và đường phân giác.

Cho tam giác ABC cân tại A, AH là đường cao kẻ từ A xuống BC. Ta có:

• HB = HC = BC / 2
• Áp dụng định lý Pythagoras trong tam giác vuông ABH: AH² + BH² = AB² => AH = √(AB² – BH²)

Alt: Tam giác cân ABC với đường cao AH, minh họa cạnh đáy BC và cạnh bên AB, giúp hình dung công thức tính đường cao.

Ví dụ:

Cho tam giác ABC cân tại A, BC = 30 cm, AB = AC = 25 cm. Tính đường cao AH.

• BH = BC / 2 = 30 / 2 = 15 cm
• AH = √(25² – 15²) = √(625 – 225) = √400 = 20 cm

Tính Chất Ba Đường Cao Của Tam Giác

Ba đường cao của một tam giác luôn cắt nhau tại một điểm, điểm này gọi là trực tâm của tam giác.

Hy vọng bài viết này cung cấp cho bạn đầy đủ thông tin và công thức để tính đường cao trong các loại tam giác khác nhau. Việc nắm vững các công thức và tính chất này sẽ giúp bạn giải quyết các bài toán hình học một cách dễ dàng và chính xác.