Công Thức Tính Độ Dài Đoạn Thẳng AB trong Mặt Phẳng Oxy
Trong hình học giải tích, việc tính độ dài đoạn thẳng AB là một bài toán cơ bản. Chúng ta sẽ xem xét công thức này trong cả mặt phẳng Oxy và không gian Oxyz.
Độ Dài Đoạn Thẳng AB Dựa Trên Tọa Độ Điểm
Cho hai điểm A và B trong mặt phẳng tọa độ Oxy. Giả sử điểm A có tọa độ $(x_A, y_A)$ và điểm B có tọa độ $(x_B, y_B)$. Khi đó, độ dài đoạn thẳng AB, ký hiệu là |AB|, được tính bằng công thức sau:
$AB = sqrt{(x_B – x_A)^2 + (y_B – y_A)^2}$
Công thức này xuất phát từ định lý Pitago, áp dụng cho tam giác vuông tạo bởi đoạn thẳng AB và các đường thẳng song song với trục Ox, Oy đi qua A và B.
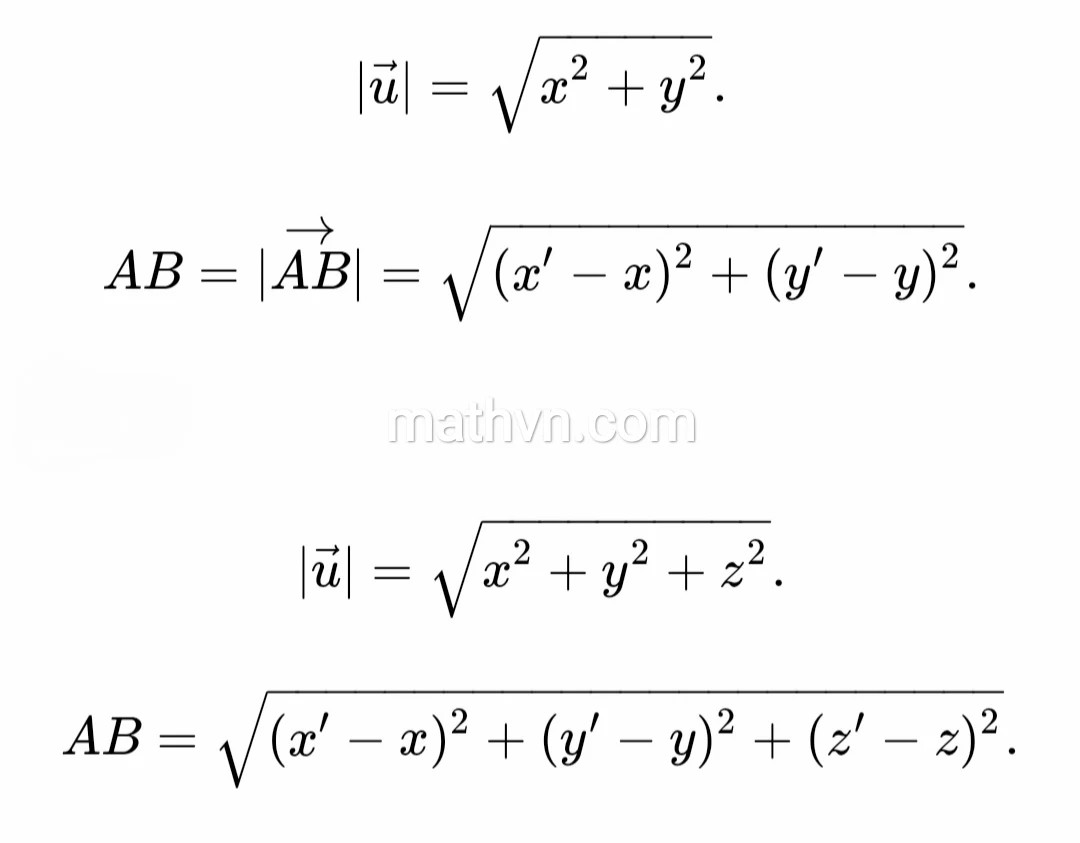Công thức tính độ dài đoạn thẳng AB trong mặt phẳng Oxy dựa trên tọa độ hai điểm A và B.
Ví Dụ Minh Họa
Ví dụ, nếu A(1; 2) và B(4; 6), thì độ dài đoạn thẳng AB là:
$AB = sqrt{(4 – 1)^2 + (6 – 2)^2} = sqrt{3^2 + 4^2} = sqrt{9 + 16} = sqrt{25} = 5$
Công Thức Tính Độ Dài Đoạn Thẳng AB trong Không Gian Oxyz
Tương tự như trong mặt phẳng, Công Thức Tính độ Dài đoạn Thẳng Ab trong không gian Oxyz cũng dựa trên tọa độ của hai điểm.
Độ Dài Đoạn Thẳng AB Dựa Trên Tọa Độ Điểm Trong Không Gian
Cho hai điểm A và B trong không gian tọa độ Oxyz. Giả sử điểm A có tọa độ $(x_A, y_A, z_A)$ và điểm B có tọa độ $(x_B, y_B, z_B)$. Khi đó, độ dài đoạn thẳng AB được tính bằng công thức sau:
$AB = sqrt{(x_B – x_A)^2 + (y_B – y_A)^2 + (z_B – z_A)^2}$
Công thức này là sự mở rộng của công thức trong mặt phẳng, bổ sung thêm thành phần z để phản ánh chiều không gian thứ ba.
Ví Dụ Minh Họa
Ví dụ, nếu A(1; 2; 3) và B(4; 6; 8), thì độ dài đoạn thẳng AB là:
$AB = sqrt{(4 – 1)^2 + (6 – 2)^2 + (8 – 3)^2} = sqrt{3^2 + 4^2 + 5^2} = sqrt{9 + 16 + 25} = sqrt{50} = 5sqrt{2}$
Ứng Dụng của Công Thức Tính Độ Dài Đoạn Thẳng AB
Công thức tính độ dài đoạn thẳng AB có nhiều ứng dụng quan trọng trong hình học giải tích và các lĩnh vực liên quan, bao gồm:
- Tính khoảng cách giữa hai điểm: Ứng dụng trực tiếp của công thức.
- Xác định tính chất của các hình: Ví dụ, kiểm tra xem một tam giác có phải là tam giác cân, tam giác đều hay tam giác vuông hay không.
- Giải các bài toán về đường tròn, mặt cầu: Tính bán kính, khoảng cách từ một điểm đến đường tròn/mặt cầu.
- Trong lập trình đồ họa: Tính khoảng cách giữa các đối tượng, xác định va chạm.
Việc nắm vững công thức tính độ dài đoạn thẳng AB là nền tảng quan trọng để giải quyết nhiều bài toán hình học và ứng dụng thực tế.
