Trong hình học, tam giác vuông đóng vai trò quan trọng và có nhiều ứng dụng thực tế. Việc tính chiều cao của tam giác vuông là một kỹ năng cơ bản. Bài viết này sẽ cung cấp đầy đủ các công thức và ví dụ minh họa để bạn nắm vững kiến thức này.
Các Công Thức Tính Chiều Cao Tam Giác Vuông
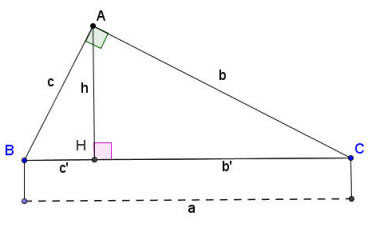
Cho tam giác ABC vuông tại A, đường cao AH vuông góc với cạnh huyền BC tại H. Ta có các công thức sau:
-
Định lý Pytago: a² = b² + c² (trong đó a là cạnh huyền, b và c là hai cạnh góc vuông).
-
Hệ thức lượng trong tam giác vuông:
- b² = a * b’ (b’ là hình chiếu của cạnh b trên cạnh huyền)
- c² = a * c’ (c’ là hình chiếu của cạnh c trên cạnh huyền)
- a h = b c (h là chiều cao AH)
- h² = b’ * c’
- 1/h² = 1/b² + 1/c²
Hình ảnh minh họa tam giác vuông ABC, giúp người đọc dễ hình dung và ghi nhớ các ký hiệu.
Trong đó:
- a, b, c lần lượt là độ dài các cạnh của tam giác vuông.
- b’ là hình chiếu của cạnh b trên cạnh huyền.
- c’ là hình chiếu của cạnh c trên cạnh huyền.
- h là chiều cao của tam giác vuông, đoạn AH vuông góc với BC.
Ví Dụ Minh Họa Chi Tiết
Ví dụ 1: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 15cm, HC = 16cm. Tính BC, AC, AH.
Hình ảnh tam giác vuông ABC với đường cao AH, giúp người đọc hiểu rõ dữ kiện bài toán.
Giải:
Áp dụng hệ thức lượng trong tam giác vuông ABC, ta có:
AC² = CH BC = 16 BC
Theo định lý Pytago: AB² + AC² = BC²
⇔ 15² + 16 * BC = BC²
⇔ BC² – 16 * BC – 225 = 0
⇔ BC² – 25 BC + 9 BC – 225 = 0
⇔ BC (BC – 25) + 9 (BC – 25) = 0
⇔ (BC – 25) (BC + 9) = 0
Vì BC > 0 => BC = 25 (cm)
=> AC² = 16 BC = 16 25 = 400 => AC = 20 (cm)
Xét tam giác vuông ABC, ta có: AH BC = AB AC (hệ thức lượng)
=> AH = (AB AC) / BC = (15 20) / 25 = 12 (cm)
Vậy: BC = 25cm, AC = 20cm, AH = 12cm
Ví dụ 2: Cho tam giác ABC vuông tại A, AB = 24cm, AC = 32cm. Tính chiều cao AH.
Giải:
Đầu tiên, tính cạnh huyền BC bằng định lý Pytago:
BC² = AB² + AC² = 24² + 32² = 576 + 1024 = 1600
=> BC = √1600 = 40 cm
Sau đó, sử dụng công thức diện tích tam giác để tính AH:
Diện tích tam giác ABC = (1/2) AB AC = (1/2) AH BC
=> AH = (AB AC) / BC = (24 32) / 40 = 19.2 cm
Ứng Dụng Thực Tế của Công Thức Tính Chiều Cao Tam Giác Vuông
Công Thức Tính Chiều Cao Tam Giác Vuông có nhiều ứng dụng trong thực tế, ví dụ:
- Xây dựng: Tính toán chiều cao của các công trình, mái nhà, v.v.
- Thiết kế: Xác định kích thước các chi tiết trong bản vẽ kỹ thuật.
- Đo đạc: Tính khoảng cách, độ cao trong địa lý và trắc địa.
- Toán học và Vật lý: Giải các bài toán liên quan đến hình học và chuyển động.
Tổng Kết
Hiểu rõ và vận dụng thành thạo các công thức tính chiều cao tam giác vuông là rất quan trọng trong học tập và công việc. Bài viết này đã cung cấp đầy đủ kiến thức cần thiết, từ công thức cơ bản đến các ví dụ minh họa và ứng dụng thực tế. Hy vọng bạn sẽ áp dụng thành công những kiến thức này.