Các Công Thức Tính Chiều Cao Tam Giác Phổ Biến
Chiều cao của tam giác là một yếu tố quan trọng trong hình học, thường được sử dụng để tính diện tích và giải quyết các bài toán liên quan. Dưới đây là các Công Thức Tính Chiều Cao Tam Giác áp dụng cho nhiều loại tam giác khác nhau.
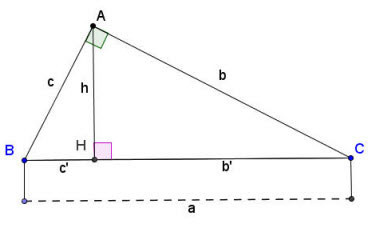
Công thức tính chiều cao tam giác thường
Công thức Heron cho phép tính diện tích tam giác khi biết độ dài ba cạnh, từ đó suy ra chiều cao.
h_a: Chiều cao kẻ từ đỉnh A xuống cạnh BC.a, b, c: Độ dài ba cạnh của tam giác.p: Nửa chu vi tam giác, được tính bằng(a + b + c) / 2.
Ví dụ:
Cho tam giác ABC có AB = 4 cm, BC = 7 cm, AC = 5 cm. Tính chiều cao AH kẻ từ A xuống BC.
Giải:
Nửa chu vi tam giác là: p = (4 + 7 + 5) / 2 = 8 cm
Chiều cao AH được tính như sau:
=>
Diện tích tam giác ABC là:
Công thức tính chiều cao tam giác đều
Tam giác đều là tam giác có ba cạnh bằng nhau. Việc tính chiều cao trong tam giác đều trở nên đơn giản hơn.
h: Chiều cao của tam giác đều.a: Độ dài cạnh của tam giác đều.
Công thức tính đường cao trong tam giác vuông
Tam giác vuông có một góc vuông (90 độ). Các công thức liên quan đến cạnh và đường cao trong tam giác vuông rất quan trọng.
Các công thức cơ bản:
a^2 = b^2 + c^2(Định lý Pythagore)b^2 = a * b'vàc^2 = a * c'(Hệ thức lượng)a * h = b * c(Hệ thức lượng)h^2 = b' * c'(Hệ thức lượng)1/h^2 = 1/b^2 + 1/c^2
Trong đó:
a, b, c: Độ dài các cạnh của tam giác vuông.b': Hình chiếu của cạnhbtrên cạnh huyềna.c': Hình chiếu của cạnhctrên cạnh huyềna.h: Chiều cao kẻ từ đỉnh góc vuông A xuống cạnh huyền BC.
Ví dụ 1: Cho tam giác ABC vuông tại A, đường cao AH. Tính BC, AC, AH biết AB = 15cm, HC = 16cm.
Giải:
Áp dụng hệ thức lượng trong tam giác vuông ABC có:
AC² = CH.BC = 16.BC
Theo định lí Pythagore cho tam giác ABC vuông tại A, ta có:
AB² + AC² = BC²
⇔ 15² + 16.BC = BC²
⇔ BC² – 16.BC – 225 = 0
⇔ BC² – 25.BC + 9.BC – 225 = 0
⇔ BC(BC – 25) + 9(BC – 25) = 0
⇔ (BC – 25)(BC + 9) = 0
⇔ BC = 25 hoặc BC = -9 (loại)
⇒ AC² = 16.BC = 16.25 = 400 ⇒ AC = 20 (cm)
Xét tam giác vuông ABC có: AH.BC = AB.AC (hệ thức lượng)
=> AH = AB.AC/BC = 15.20/25 = 12 (cm)
Vậy BC = 25 cm; AC = 20 cm; AH = 12 cm.
Ví dụ 2:
Cho tam giác ABC vuông tại A, AB = 24cm, AC = 32cm. Đường trung trực của BC cắt AC, BC theo thứ tự D và E. Tính DE.
Giải:
Xét tam giác vuông ABC, ta có:
BC² = AB² + AC² (theo định lý Pythagore)
BC² = 24² + 32²
BC² = 1600
BC = 40 (cm)
EC = BC : 2 = 40 : 2 = 20 (cm)
Xét tam giác vuông ACB và tam giác vuông ECD có:
∠A = ∠E = 90°
∠C chung
=> Tam giác ACB đồng dạng tam giác ECD (g.g)
=> AC/EC = AB/ED
=> ED = AB.EC/AC = 15cm
Vậy ED = 15cm
Công thức tính đường cao trong tam giác cân
Tam giác cân là tam giác có hai cạnh bằng nhau. Đường cao trong tam giác cân có tính chất đặc biệt.
Giả sử tam giác ABC cân tại A, đường cao AH vuông góc tại H như hình trên:
Công thức tính đường cao AH:
Vì tam giác ABC cân tại A nên đường cao AH đồng thời là đường trung tuyến, suy ra:
⇒ HB = HC = BC / 2
Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:
AH² + BH² = AB²
⇒ AH² = AB² − BH²
Ví dụ: Cho Δ ABC cân tại A có BC = 30 cm, đường cao AH = 20 cm. Tính đường cao ứng với cạnh bên của tam giác cân đó.
Giải:
Xét Δ ABC cân tại A có BC = 30 cm
⇒ BH = CH = 15 cm.
Áp dụng định lý Py – ta – go ta có:
Kẻ BK ⊥ AC, giờ ta phải tính BK = ?
Ta có:
Mặt khác
Do đó, ta có ⇔
Định Nghĩa Đường Cao Tam Giác
Đường cao trong tam giác là đoạn thẳng vuông góc kẻ từ một đỉnh của tam giác xuống cạnh đối diện. Cạnh đối diện này được gọi là đáy tương ứng với đường cao đó.
Tính Chất Ba Đường Cao Trong Tam Giác
Ba đường cao của một tam giác luôn cắt nhau tại một điểm, điểm này được gọi là trực tâm của tam giác.
Việc nắm vững các công thức và tính chất trên sẽ giúp bạn dễ dàng giải quyết các bài toán liên quan đến chiều cao trong tam giác.