Trong chương trình hình học không gian THPT, việc nắm vững Công Thức Tính Chiều Cao Khối Chóp là vô cùng quan trọng để giải quyết các bài toán liên quan đến thể tích và các yếu tố hình học khác. Bài viết này sẽ tổng hợp và trình bày chi tiết các công thức, phương pháp xác định chiều cao, cùng các ví dụ minh họa giúp bạn đọc hiểu rõ và áp dụng hiệu quả.
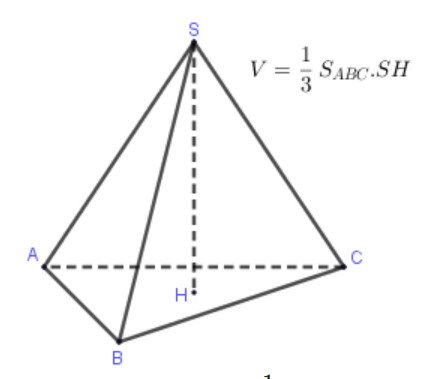
Hình ảnh minh họa trực quan về khối chóp, các thành phần đáy, đỉnh và chiều cao, giúp người đọc dễ dàng hình dung và ghi nhớ khái niệm.
1. Công Thức Tính Thể Tích Khối Chóp Cơ Bản và Suy Ra Chiều Cao
Công thức tính thể tích khối chóp tổng quát là:
V = (1/3) S h
Trong đó:
- V là thể tích khối chóp
- S là diện tích đáy
- h là chiều cao của khối chóp (khoảng cách từ đỉnh đến mặt đáy)
Từ công thức trên, ta có thể suy ra công thức tính chiều cao khối chóp khi biết thể tích và diện tích đáy:
h = (3 * V) / S
Đây là công thức quan trọng nhất và được sử dụng phổ biến để tính chiều cao khi các yếu tố khác đã được xác định.
2. Các Trường Hợp Đặc Biệt và Cách Xác Định Chiều Cao
2.1. Khối Chóp Có Mặt Bên Vuông Góc Với Đáy
Nếu khối chóp có một hoặc nhiều mặt bên vuông góc với đáy, thì chiều cao của khối chóp chính là đường cao của mặt bên đó hạ từ đỉnh xuống giao tuyến của mặt bên và mặt đáy.
Hình ảnh mô tả khối chóp với mặt bên vuông góc đáy, chỉ rõ đường cao của mặt bên đó chính là chiều cao của khối chóp, giúp người học nhận diện và áp dụng công thức một cách chính xác.
Ví dụ: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, mặt phẳng (SBC) vuông góc với (ABC). Chiều cao của khối chóp là đường cao SH của tam giác SBC (với H thuộc BC).
2.2. Khối Chóp Có Cạnh Bên Vuông Góc Với Đáy
Nếu khối chóp có một cạnh bên vuông góc với đáy, thì cạnh bên đó chính là chiều cao của khối chóp.
Ví dụ: Cho hình chóp S.ABC có SA vuông góc với đáy (ABC). Khi đó, SA là chiều cao của khối chóp.
Hình ảnh trực quan về khối chóp với cạnh bên vuông góc đáy, giúp người học dễ dàng nhận biết và áp dụng công thức tính chiều cao trong trường hợp đặc biệt này.
2.3. Khối Chóp Đều
Khối chóp đều là khối chóp có đáy là đa giác đều và chân đường cao hạ từ đỉnh xuống đáy trùng với tâm của đa giác đáy. Để tìm chiều cao, ta có thể sử dụng định lý Pythagoras trong tam giác vuông tạo bởi chiều cao, cạnh bên và bán kính đường tròn ngoại tiếp đáy.
3. Ví Dụ Minh Họa Tính Chiều Cao Khối Chóp
Ví dụ 1: Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, thể tích khối chóp là V = (a³√2) / 6. Tính chiều cao của khối chóp.
Giải:
- Diện tích đáy: S = a²
- Áp dụng công thức: h = (3 V) / S = (3 (a³√2) / 6) / a² = (a√2) / 2
Ví dụ 2: Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với đáy và SA = a√3. Tính chiều cao của khối chóp.
Giải:
- Vì SA vuông góc với đáy, nên chiều cao của khối chóp là SA = a√3.
4. Lưu Ý Quan Trọng Khi Tính Chiều Cao Khối Chóp
- Xác định chính xác vị trí chân đường cao: Đây là yếu tố then chốt để tìm ra chiều cao.
- Sử dụng các định lý và tính chất hình học: Định lý Pythagoras, tính chất tam giác đồng dạng, các hệ thức lượng trong tam giác…
- Phân tích kỹ đề bài: Nhận diện các yếu tố đặc biệt của khối chóp (mặt bên vuông góc, cạnh bên vuông góc, chóp đều…) để áp dụng công thức phù hợp.
5. Ứng Dụng của Công Thức Tính Chiều Cao Khối Chóp
Việc tính chiều cao khối chóp không chỉ giúp tính thể tích mà còn có vai trò quan trọng trong việc giải các bài toán liên quan đến:
- Tính khoảng cách từ một điểm đến một mặt phẳng.
- Xác định góc giữa đường thẳng và mặt phẳng.
- Chứng minh các tính chất hình học.
Hình ảnh minh họa bài tập luyện tập thể tích hình chóp, giúp người học áp dụng kiến thức đã học vào giải quyết các bài toán cụ thể, nâng cao kỹ năng và hiểu sâu sắc hơn về công thức tính chiều cao khối chóp.
Nắm vững công thức tính chiều cao khối chóp và các phương pháp xác định chiều cao trong các trường hợp đặc biệt là nền tảng vững chắc để chinh phục các bài toán hình học không gian. Hãy luyện tập thường xuyên để thành thạo và tự tin giải quyết mọi thử thách!