Khối lăng trụ tam giác đều là một hình học quan trọng trong chương trình toán phổ thông và có nhiều ứng dụng thực tế. Bài viết này sẽ cung cấp đầy đủ kiến thức về hình lăng trụ tam giác đều, tập trung vào công thức tính thể tích, kèm theo các bài tập minh họa có lời giải chi tiết.
1. Định Nghĩa và Tính Chất của Lăng Trụ Tam Giác Đều
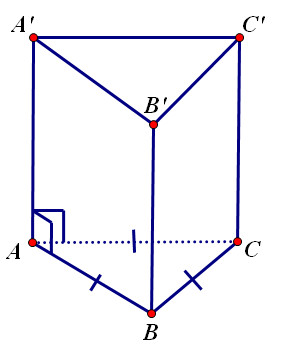
Lăng trụ tam giác đều là hình lăng trụ đứng có hai đáy là hai tam giác đều bằng nhau.
Alt: Hình lăng trụ tam giác đều với đáy là tam giác đều và các mặt bên là hình chữ nhật, thể hiện rõ cấu trúc hình học.
Các tính chất quan trọng:
- Hai đáy là hai tam giác đều có kích thước bằng nhau.
- Các cạnh bên bằng nhau và vuông góc với mặt đáy.
- Các mặt bên là các hình chữ nhật bằng nhau.
2. Công Thức Tính Thể Tích Khối Lăng Trụ Tam Giác Đều
Thể tích của khối lăng trụ tam giác đều được tính bằng công thức:
*V = S h**
Trong đó:
- V: Thể tích của khối lăng trụ (đơn vị: mét khối – m³).
- S: Diện tích đáy của khối lăng trụ (diện tích tam giác đều) (đơn vị: mét vuông – m²).
- h: Chiều cao của khối lăng trụ (khoảng cách giữa hai đáy) (đơn vị: mét – m).
Vì đáy là tam giác đều cạnh a, diện tích đáy được tính như sau:
*S = (a² √3) / 4**
Do đó, công thức tính thể tích có thể viết lại là:
V = (a² √3 h) / 4
Alt: Biểu thức toán học thể hiện công thức tính thể tích khối lăng trụ tam giác đều, nhấn mạnh mối liên hệ giữa diện tích đáy, chiều cao và thể tích.
3. Công Thức Tính Diện Tích Xung Quanh và Diện Tích Toàn Phần
3.1. Diện Tích Xung Quanh (Sxq)
Diện tích xung quanh của lăng trụ tam giác đều bằng tổng diện tích của ba mặt bên hình chữ nhật. Vì ba mặt bên bằng nhau, ta có:
*Sxq = P h = 3 a h**
Trong đó:
- P: Chu vi đáy (tam giác đều).
- a: Độ dài cạnh đáy.
- h: Chiều cao của lăng trụ.
3.2. Diện Tích Toàn Phần (Stp)
Diện tích toàn phần của lăng trụ tam giác đều bằng tổng diện tích xung quanh và diện tích hai đáy:
Stp = Sxq + 2 Sđáy = 3 a h + 2 (a² √3) / 4 = 3 a h + (a² √3) / 2
4. Bài Tập Vận Dụng và Lời Giải Chi Tiết
Bài 1: Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy a = 4cm và chiều cao h = 6cm. Tính thể tích của lăng trụ.
Giải:
Áp dụng công thức: V = (a² √3 h) / 4
Thay số: V = (4² √3 6) / 4 = (16 √3 6) / 4 = 24√3 cm³
Bài 2: Một lăng trụ tam giác đều có thể tích là 36√3 cm³ và cạnh đáy là 6cm. Tính chiều cao của lăng trụ.
Giải:
Áp dụng công thức: V = (a² √3 h) / 4 => h = (4 V) / (a² √3)
Thay số: h = (4 36√3) / (6² √3) = (144√3) / (36√3) = 4 cm
Bài 3: Cho lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng 5cm. Tính thể tích của lăng trụ.
Giải:
Vì tất cả các cạnh bằng nhau, suy ra a = h = 5cm.
Áp dụng công thức: V = (a² √3 h) / 4
Thay số: V = (5² √3 5) / 4 = (25 √3 5) / 4 = (125√3) / 4 cm³
Bài 4: Tính diện tích xung quanh và diện tích toàn phần của một lăng trụ tam giác đều có cạnh đáy là 3cm và chiều cao là 5cm.
Giải:
- Diện tích xung quanh: Sxq = 3 a h = 3 3 5 = 45 cm²
- Diện tích toàn phần: Stp = 3 a h + (a² √3) / 2 = 45 + (3² √3) / 2 = 45 + (9√3) / 2 cm²
Bài 5: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng 8cm và mặt phẳng (A’BC) tạo với đáy (ABC) một góc 60°. Tính thể tích khối lăng trụ ABC.A’B’C’.
Giải:
Gọi I là trung điểm của BC. Vì tam giác ABC đều, ta có AI ⊥ BC. Tương tự, A’I ⊥ BC (vì A’BC là tam giác cân). Góc giữa (A’BC) và (ABC) là góc A’IA = 60°.
Trong tam giác vuông A’AI, ta có: AA’ = AI * tan(60°)
AI = (a√3)/2 = (8√3)/2 = 4√3 cm
AA’ = 4√3 * √3 = 12 cm
Diện tích đáy ABC: S(ABC) = (a²√3)/4 = (8²√3)/4 = 16√3 cm²
Thể tích khối lăng trụ: V = AA’ S(ABC) = 12 16√3 = 192√3 cm³
5. Ứng Dụng Thực Tế
Công thức tính thể tích khối lăng trụ tam giác đều không chỉ quan trọng trong học tập mà còn có nhiều ứng dụng thực tế trong kiến trúc, xây dựng, thiết kế, và sản xuất. Ví dụ, trong xây dựng, việc tính toán thể tích giúp xác định lượng vật liệu cần thiết cho các cấu trúc có hình dạng lăng trụ tam giác đều.
Hy vọng bài viết này cung cấp cho bạn kiến thức đầy đủ và chi tiết về công thức tính thể tích khối lăng trụ tam giác đều, giúp bạn áp dụng hiệu quả vào học tập và công việc.