Công Thức Sin Cos Lớp 9 là một phần kiến thức quan trọng trong chương trình Toán THCS. Việc nắm vững và vận dụng thành thạo các công thức này không chỉ giúp các em học sinh giải quyết tốt các bài toán liên quan mà còn tạo nền tảng vững chắc cho việc học Toán ở các cấp học cao hơn. Bài viết này sẽ tổng hợp đầy đủ các công thức sin cos lớp 9 cần nhớ, kèm theo ví dụ minh họa và bài tập áp dụng để giúp các em học sinh dễ dàng nắm bắt và vận dụng kiến thức.
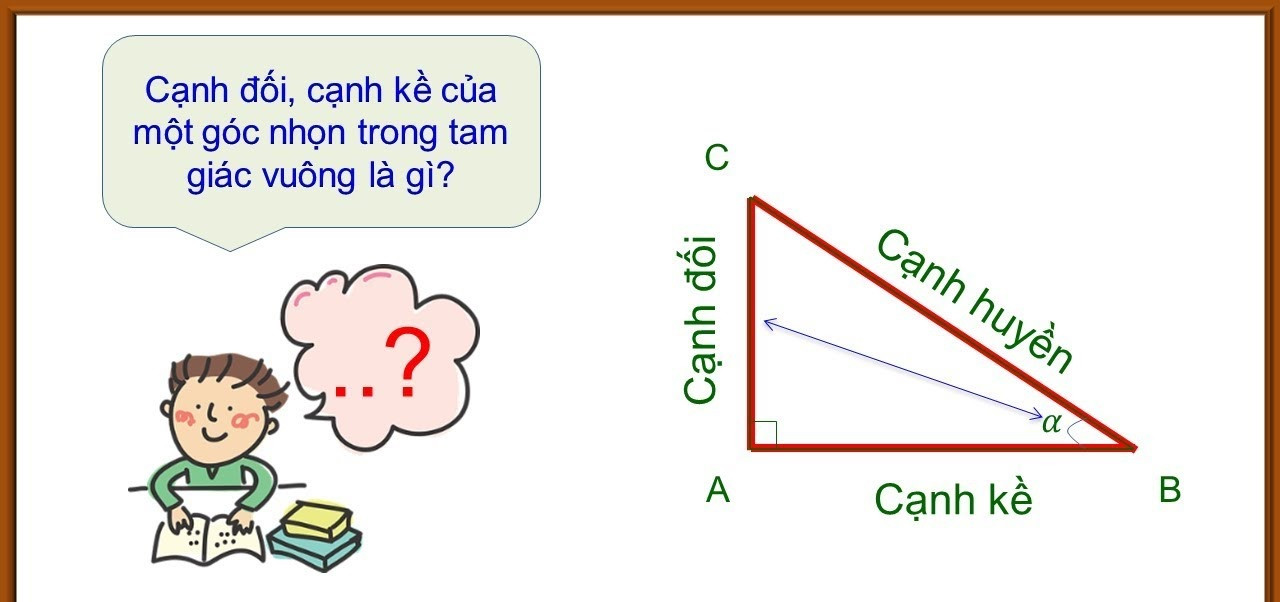
1. Tỉ Số Lượng Giác Của Góc Nhọn Trong Tam Giác Vuông
Trong tam giác vuông, các tỉ số lượng giác của một góc nhọn được định nghĩa như sau:
- Sin (sinus) của một góc nhọn là tỉ số giữa cạnh đối và cạnh huyền.
- Cos (cosinus) của một góc nhọn là tỉ số giữa cạnh kề và cạnh huyền.
- Tan (tang) của một góc nhọn là tỉ số giữa cạnh đối và cạnh kề.
- Cot (cotang) của một góc nhọn là tỉ số giữa cạnh kề và cạnh đối.
Các công thức lượng giác lớp 9 cơ bản cần ghi nhớ.
Công thức:
Cho tam giác ABC vuông tại A, góc B là góc nhọn:
- sin B = AC/BC (cạnh đối / cạnh huyền)
- cos B = AB/BC (cạnh kề / cạnh huyền)
- tan B = AC/AB (cạnh đối / cạnh kề)
- cot B = AB/AC (cạnh kề / cạnh đối)
Mẹo nhớ nhanh: “Sin đi học, Cos không hư, Tan đoàn kết, Cot kết đoàn”
2. Quan Hệ Giữa Các Tỉ Số Lượng Giác Của Hai Góc Phụ Nhau
Hai góc được gọi là phụ nhau nếu tổng của chúng bằng 90°. Giữa các tỉ số lượng giác của hai góc phụ nhau có mối quan hệ sau:
- sin α = cos (90° – α)
- cos α = sin (90° – α)
- tan α = cot (90° – α)
- cot α = tan (90° – α)
Ví dụ: sin 30° = cos 60°; tan 45° = cot 45°
3. Bảng Giá Trị Lượng Giác Của Các Góc Đặc Biệt
Việc ghi nhớ bảng giá trị lượng giác của các góc đặc biệt (0°, 30°, 45°, 60°, 90°) là rất quan trọng để giải các bài toán lượng giác một cách nhanh chóng và chính xác.
| Góc α | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| sin α | 0 | 1/2 | √2/2 | √3/2 | 1 |
| cos α | 1 | √3/2 | √2/2 | 1/2 | 0 |
| tan α | 0 | √3/3 | 1 | √3 | Không xác định |
| cot α | Không xác định | √3 | 1 | √3/3 | 0 |

Bảng giá trị sin cos của các góc đặc biệt thường gặp trong chương trình lớp 9.
4. Các Hệ Thức Lượng Giác Cơ Bản
Ngoài các định nghĩa và quan hệ trên, các em cần nắm vững các hệ thức lượng giác cơ bản sau:
- sin²α + cos²α = 1
- tan α = sin α / cos α (với cos α ≠ 0)
- cot α = cos α / sin α (với sin α ≠ 0)
- tan α . cot α = 1 (với sin α ≠ 0 và cos α ≠ 0)
5. Ứng Dụng Các Hệ Thức Về Cạnh Và Góc Trong Tam Giác Vuông
Trong tam giác vuông, các cạnh và góc có mối quan hệ chặt chẽ thông qua các tỉ số lượng giác.
Cho tam giác ABC vuông tại A:
- b = a . sin B = a . cos C
- c = a . sin C = a . cos B
- b = c . tan B = c . cot C
- c = b . tan C = b . cot B
Trong đó:
- a là cạnh huyền (BC)
- b là cạnh đối diện góc B (AC)
- c là cạnh đối diện góc C (AB)
Tam giác vuông ABC và các ký hiệu cạnh góc để áp dụng công thức lượng giác.
6. Bài Tập Vận Dụng
Ví dụ 1: Cho tam giác ABC vuông tại A, biết AB = 3 cm, AC = 4 cm. Tính sin B, cos B, tan B, cot B.
Giải:
Áp dụng định lý Py-ta-go, ta có: BC² = AB² + AC² = 3² + 4² = 25 => BC = 5 cm
- sin B = AC/BC = 4/5
- cos B = AB/BC = 3/5
- tan B = AC/AB = 4/3
- cot B = AB/AC = 3/4
Ví dụ 2: Cho góc α thỏa mãn sin α = 0.6. Tính cos α, tan α, cot α.
Giải:
- cos²α = 1 – sin²α = 1 – 0.6² = 0.64 => cos α = 0.8 (vì α là góc nhọn nên cos α > 0)
- tan α = sin α / cos α = 0.6 / 0.8 = 0.75
- cot α = 1 / tan α = 1 / 0.75 = 4/3
Bài tập tự luyện:
- Cho tam giác ABC vuông tại A, biết góc B = 60°, AB = 5 cm. Tính AC và BC.
- Cho góc α thỏa mãn cos α = 0.8. Tính sin α, tan α, cot α.
- Chứng minh rằng trong tam giác vuông, sin²B + cos²B = 1 (với B là một góc nhọn).
Nắm vững các công thức sin cos lớp 9 và luyện tập thường xuyên sẽ giúp các em học sinh tự tin hơn khi giải các bài toán liên quan và đạt kết quả tốt trong học tập. Chúc các em học tốt!