Để giải quyết các bài toán liên quan đến phương trình logarit một cách hiệu quả, việc nắm vững lý thuyết và các công thức là vô cùng quan trọng. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về các Công Thức Phương Trình Logarit, các dạng bài tập thường gặp và phương pháp giải phù hợp.
Tổng quan về phương trình logarit và ứng dụng thực tế trong toán học và các lĩnh vực liên quan.
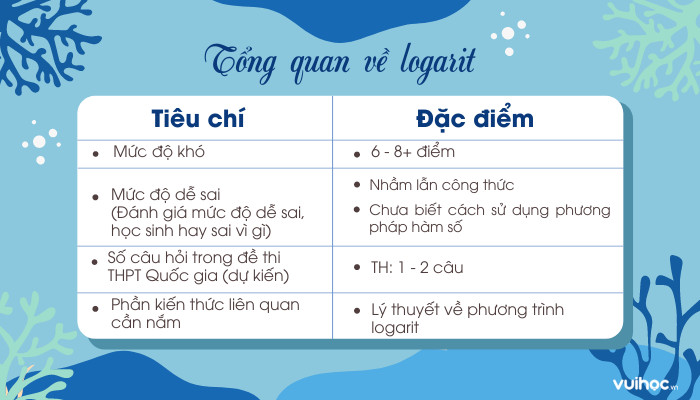
1. Tổng Quan Về Logarit và Phương Trình Logarit
1.1. Lý Thuyết Logarit Cần Nhớ
Logarit của một số là số mũ mà cơ số phải được nâng lên để tạo ra số đó. Hiểu một cách đơn giản, logarit là phép toán nghịch đảo của lũy thừa.
Ví dụ: logarit cơ số 10 của 100 là 2 vì 102 = 100. Tổng quát, nếu x = by thì y được gọi là logarit cơ số b của x, ký hiệu là logbx.
Các loại logarit thường gặp:
- Logarit thập phân: Cơ số 10, ký hiệu log10b = log b (=lgb).
- Logarit tự nhiên: Cơ số e (≈ 2.718), ký hiệu ln(b), loge(b).
- Logarit nhị phân: Cơ số 2, ký hiệu log2b.
Công thức chung: logab với b > 0, 0 < a ≠ 1.
Các công thức logarit quan trọng:
- Tích: loga(bc) = logab + logac
- Thương: loga(b/c) = logab – logac
- Lũy thừa: logabn = n.logab
- Đổi cơ số: logbx = logkx / logkb
Công thức logarit cơ bản về tích, thương, lũy thừa và căn thức giúp biến đổi và giải các bài toán logarit.
Công thức đổi cơ số logarit, cho phép chuyển đổi giữa các cơ số khác nhau.
Công thức tính logarit cơ số b bất kỳ dựa trên logarit cơ số 10 hoặc e, thường sử dụng trong tính toán.
1.2. Phương Trình Logarit Cơ Bản
Phương trình logarit cơ bản có dạng: logax = b (với a > 0, a ≠ 1).
Phương trình này luôn có nghiệm duy nhất: x = ab.
Điều kiện xác định: Biểu thức trong logarit phải lớn hơn 0.
Quy tắc quan trọng:
- Logarit của một tích: logα(ab) = logαb + logαc (a, b, c > 0, a ≠ 1).
- Logarit của một lũy thừa: logabα = αlogab (a, b > 0, a ≠ 1).
Công thức phương trình logarit cơ bản với điều kiện xác định và nghiệm của phương trình.
Lưu ý về điều kiện và công thức biến đổi phương trình logarit, giúp giải toán chính xác hơn.
2. Tổng Hợp Công Thức Logarit Quan Trọng
2.1. Bảng Công Thức Logarit Cơ Bản
| Công Thức | Giải Thích |
|---|---|
| loga1 = 0 | Logarit của 1 luôn bằng 0. |
| logaa = 1 | Logarit của cơ số bằng 1. |
| logaam = m | Logarit của lũy thừa của cơ số. |
| alogan = n | Mũ của logarit cơ số a. |
| loga(n1.n2) = logan1 + logan2 | Logarit của tích. |
| loga (n1/n2) = logan1 – logan2 | Logarit của thương. |
| logaNα = α .logaN | Logarit của lũy thừa. |
| logaN2 = 2.loga | N |
| logaN = logba.logbN | Đổi cơ số. |
| logbN = (logaN) / (logab) | Đổi cơ số (tiếp). |
| logab = 1 / logba | Nghịch đảo của logarit. |
| logaαN = (1/α)logaN | Logarit với cơ số lũy thừa. |
| alogbc = clogba | Hoán đổi vị trí. |


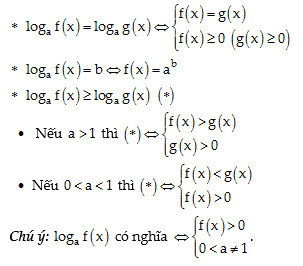



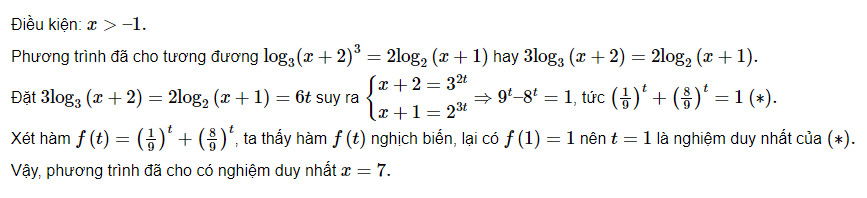
2.2. Công Thức Lũy Thừa Cần Thiết
| Công Thức | Giải Thích |
|---|---|
| a0 = 1 | Mọi số mũ 0 đều bằng 1. |
| a1 = a | Mọi số mũ 1 đều bằng chính nó. |
| a-α = 1/aα | Số mũ âm. |
| aα . aβ = aα+β | Nhân lũy thừa cùng cơ số. |
| aα / aβ = aα – β | Chia lũy thừa cùng cơ số. |
| aα . bα = (a.b)α | Nhân lũy thừa cùng số mũ. |
| aα / bα = (a/b)α (b≠ 0) | Chia lũy thừa cùng số mũ. |
| aα/β = β√aα (β ∈ N*) | Lũy thừa hữu tỉ. |
| aα = b ⇒ α = loga b | Định nghĩa logarit. |
| (aα)β = aα.β | Lũy thừa của lũy thừa. |
2.3. Công Thức Đạo Hàm Logarit
- Cơ bản:
- (lnx)’ = 1/x
- (logax)’ = 1/(x.lna)
- Hàm hợp:
- (lnu)’ = u’/u
- (logau)’ = u’/(u.lna)
2.4. Công Thức Đổi Cơ Số Logarit
- logab = (logcb) / (logca) (∀ a, b, c > 0 và a, c ≠ 1)
- logaαb = (1/α) logab (∀ a,b > 0 và a ≠ 1)
3. Các Dạng Bài Tập Phương Trình Logarit và Cách Giải
3.1. Đưa Về Cùng Cơ Số
Phương pháp này dựa trên việc biến đổi phương trình về dạng logaf(x) = logag(x) hoặc logaf(x) = b.
- Trường hợp 1: logaf(x) = b => f(x) = ab
- Trường hợp 2: logaf(x) = logag(x) <=> f(x) = g(x)
Ví dụ: Giải phương trình log2(x – 1) = 3
- Điều kiện: x > 1
- Áp dụng công thức: x – 1 = 23
- => x – 1 = 8
- => x = 9 (thỏa mãn điều kiện)
Ví dụ minh họa phương pháp giải phương trình logarit bằng cách đưa về cùng cơ số.
3.2. Đặt Ẩn Phụ
Phương pháp này giúp đơn giản hóa phương trình bằng cách thay thế biểu thức logarit bằng một biến mới.
- Phương trình dạng: Q[logaf(x)] = 0 => Đặt t = logax (x thuộc R)
Ví dụ: Giải phương trình (log2x)2 – 3log2x + 2 = 0
- Đặt t = log2x
- Phương trình trở thành: t2 – 3t + 2 = 0
- Giải phương trình bậc hai: t = 1 hoặc t = 2
- Với t = 1 => log2x = 1 => x = 2
- Với t = 2 => log2x = 2 => x = 4
Ví dụ minh họa phương pháp đặt ẩn phụ để giải phương trình logarit.
3.3. Mũ Hóa
Mũ hóa hai vế phương trình với cơ số thích hợp để loại bỏ logarit.
- logaf(x) = logbg(x) => Đặt logaf(x) = logbg(x) = t => f(x) = at hoặc g(x) = bt
Ví dụ: Giải phương trình log2(x + 1) = log4(3x + 7)
- Đổi cơ số: log2(x + 1) = log22(3x + 7) = (1/2)log2(3x + 7)
- => 2log2(x + 1) = log2(3x + 7)
- => log2(x + 1)2 = log2(3x + 7)
- => (x + 1)2 = 3x + 7
- => x2 – x – 6 = 0
- => x = 3 hoặc x = -2
- Kiểm tra điều kiện: x = 3 (thỏa mãn), x = -2 (loại)
Ví dụ minh họa phương pháp mũ hóa để giải phương trình logarit.
3.4. Sử Dụng Đồ Thị
Giải phương trình logax = f(x) bằng cách vẽ đồ thị hai hàm số y = logax và y = f(x), sau đó tìm giao điểm. Số giao điểm là số nghiệm của phương trình.
Bước 1: Vẽ đồ thị các hàm số y = logax (0 < a ≠ 1) và y = f(x) trên cùng một hệ trục tọa độ.
Bước 2: Xác định số giao điểm của hai đồ thị.
Bước 3: Kết luận nghiệm của phương trình.
Ví dụ minh họa phương pháp sử dụng đồ thị để tìm nghiệm của phương trình logarit.
Ví dụ về đồ thị hàm số logarit và đường thẳng để minh họa cách tìm nghiệm.
Nắm vững lý thuyết và các phương pháp giải phương trình logarit là chìa khóa để thành công trong các bài kiểm tra và kỳ thi. Hãy luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau và nâng cao kỹ năng giải toán. Chúc các bạn học tốt!