Mặt cầu ngoại tiếp hình chóp là một chủ đề quan trọng trong hình học không gian, xuất hiện nhiều trong các kỳ thi. Bài viết này sẽ cung cấp đầy đủ và chi tiết về định nghĩa, phương pháp tìm tâm, bán kính và các dạng bài tập thường gặp liên quan đến mặt cầu ngoại tiếp hình chóp, giúp bạn nắm vững kiến thức và tự tin giải mọi bài toán.
1. Định Nghĩa Mặt Cầu Ngoại Tiếp Hình Chóp
Mặt cầu ngoại tiếp hình chóp (hay hình chóp nội tiếp mặt cầu) là mặt cầu đi qua tất cả các đỉnh của hình chóp đó. Nói cách khác, hình chóp nằm hoàn toàn bên trong mặt cầu và các đỉnh của nó tiếp xúc với mặt cầu.
2. Phương Pháp Xác Định Tâm và Bán Kính Mặt Cầu Ngoại Tiếp
Để tìm tâm và bán kính mặt cầu ngoại tiếp hình chóp, ta thường sử dụng các bước sau:
- Xác định tâm đường tròn ngoại tiếp đa giác đáy: Gọi tâm đường tròn ngoại tiếp đa giác đáy là O.
- Dựng trục của đường tròn ngoại tiếp đáy: Dựng đường thẳng d vuông góc với mặt phẳng đáy tại O. Đường thẳng d này gọi là trục của đường tròn ngoại tiếp đáy.
- Xác định mặt phẳng trung trực của một cạnh bên (hoặc trục của đường tròn ngoại tiếp một mặt bên): Chọn một cạnh bên bất kỳ (ví dụ SA) và dựng mặt phẳng trung trực (P) của cạnh đó. Hoặc xác định trục của đường tròn ngoại tiếp một mặt bên.
- Tìm giao điểm: Giao điểm I của trục d và mặt phẳng (P) (hoặc giao điểm của hai trục) chính là tâm của mặt cầu ngoại tiếp hình chóp.
- Tính bán kính: Bán kính R của mặt cầu ngoại tiếp hình chóp là khoảng cách từ tâm I đến một đỉnh bất kỳ của hình chóp (ví dụ R = IA).
3. Công Thức Tính Nhanh Bán Kính Mặt Cầu Ngoại Tiếp Hình Chóp
Để giải nhanh các bài toán trắc nghiệm, bạn có thể tham khảo bảng công thức sau:
| Dạng Toán | Bán Kính Mặt Cầu Ngoại Tiếp (R) |
|---|---|
| Đa diện có các đỉnh nhìn đoạn AB dưới một góc 90 độ | $R = frac{AB}{2}$ |
| Hình chóp đều có cạnh bên SA, chiều cao SO | $R = frac{SA^2}{2SO}$ |
| Hình chóp có cạnh h = SA vuông góc với đáy và bán kính đường tròn ngoại tiếp đáy là r | $R = sqrt{r^2 + frac{h^2}{4}}$ |
| Hình chóp có mặt bên SAB là tam giác đều cạnh AB, bán kính đường tròn ngoại tiếp đáy là $R_d$ | $R = sqrt{R_b^2 + R_d^2 – frac{AB^2}{4}}$ (Với $R_b$ là bán kính đường tròn ngoại tiếp tam giác SAB) |
4. Các Dạng Toán Thường Gặp và Ví Dụ Minh Họa
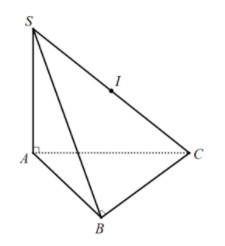
4.1. Hình Chóp Có Các Điểm Cùng Nhìn Một Đoạn Thẳng AB Dưới Một Góc Vuông
Phương pháp:
- Xác định tâm I là trung điểm của đoạn thẳng AB.
- Bán kính R = $frac{AB}{2}$
Ví dụ:
Cho hình chóp S.ABC có đường cao SA, đáy ABC là tam giác vuông tại B. Biết $widehat{SAC} = widehat{SBC} = 90^circ$. Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABC.
Giải:
Vì A và B cùng nhìn SC dưới một góc vuông, nên mặt cầu ngoại tiếp hình chóp S.ABC có:
- Tâm I là trung điểm của SC.
- Bán kính R = $frac{SC}{2}$.
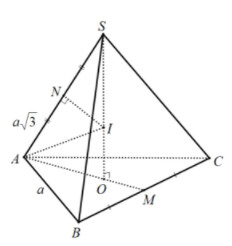
4.2. Hình Chóp Đều
Phương pháp:
- Gọi O là tâm của đa giác đáy. Suy ra SO là trục của đường tròn ngoại tiếp đa giác đáy.
- Trong mặt phẳng (SAO), vẽ đường trung trực của SA cắt SO tại I. Khi đó, I là tâm mặt cầu ngoại tiếp hình chóp.
- Sử dụng công thức: $R = frac{SA^2}{2SO}$ (với SA là cạnh bên, SO là chiều cao).
Ví dụ:
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, cạnh bên SA = $asqrt{3}$. Tính bán kính mặt cầu ngoại tiếp hình chóp đó.
Giải:
Gọi O là tâm của tam giác đều ABC. Suy ra SO vuông góc với (ABC) và SO là trục của đường tròn ngoại tiếp tam giác ABC.
Gọi N là trung điểm SA. Trong mặt phẳng (SAO), kẻ đường trung trực của SA cắt SO tại I. Khi đó, I là tâm của mặt cầu ngoại tiếp hình chóp S.ABC.
Bán kính R = SI. Vì $Delta SNI sim Delta SOA$, nên $frac{SN}{SO} = frac{SI}{SA}$.
=> $R = SI = frac{SN.SA}{SO} = frac{SA^2}{2SO} = frac{3asqrt{6}}{8}$.
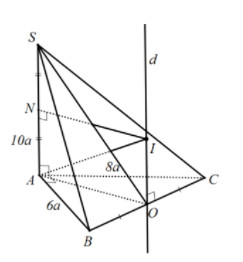
4.3. Hình Chóp Có Cạnh Bên Vuông Góc Với Mặt Phẳng Đáy
Phương pháp:
- Gọi O là tâm đường tròn ngoại tiếp đa giác đáy. Dựng đường thẳng d vuông góc với mặt phẳng đáy tại O.
- Trong mặt phẳng (d, SA), dựng đường trung trực của cạnh SA cắt d tại I. Khi đó, I là tâm của mặt cầu ngoại tiếp hình chóp.
- Sử dụng công thức: $R = sqrt{r^2 + left(frac{SA}{2}right)^2}$, với r là bán kính đường tròn ngoại tiếp đáy.
Ví dụ:
Cho hình chóp S.ABC có cạnh SA vuông góc với mặt đáy, ABC là tam giác vuông tại A, có AB = 6a, AC = 8a, SA = 10a. Tính độ dài bán kính của mặt cầu ngoại tiếp hình chóp S.ABC.
Giải:
Gọi O là trung điểm BC. Suy ra O là tâm của đường tròn ngoại tiếp tam giác ABC. Dựng trục d của đường tròn ngoại tiếp ABC. Trong mặt phẳng (SA, d), vẽ trung trực của cạnh SA cắt d tại I.
Khi đó, I là tâm của mặt cầu ngoại tiếp hình chóp S.ABC và bán kính R = IA = IB = IS.
Ta có tứ giác NIOA là hình chữ nhật.
Xét tam giác NAI vuông tại N, ta có:
$R = IA = sqrt{NI^2 + NA^2} = sqrt{left(frac{BC}{2}right)^2 + left(frac{SA}{2}right)^2} = sqrt{left(frac{AB^2 + AC^2}{4}right) + left(frac{SA}{2}right)^2} = 5asqrt{2}$.
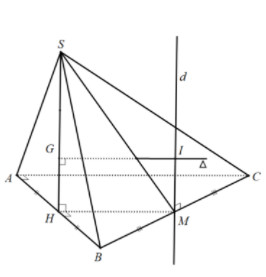
4.4. Hình Chóp Có Mặt Bên Vuông Góc Với Mặt Phẳng Đáy
Phương pháp:
- Xác định trục d của đường tròn ngoại tiếp đáy.
- Xác định trục ∆ của đường tròn ngoại tiếp mặt bên vuông góc với đáy.
- Tìm giao điểm I của d và ∆. I là tâm mặt cầu ngoại tiếp hình chóp.
Ví dụ:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Mặt bên (SAB) vuông góc với mặt (ABC) và SAB đều cạnh bằng 1. Tìm độ dài bán kính mặt cầu ngoại tiếp hình chóp tam giác S.ABC.
Giải:
Gọi H, M lần lượt là trung điểm của AB, AC.
M là tâm đường tròn ngoại tiếp tam giác ABC (vì MA = MB = MC).
Dựng d là trục của đường tròn ngoại tiếp tam giác ABC (d qua M và song song với SH).
G là tâm đường tròn ngoại tiếp tam giác SAB và ∆ là trục đường tròn ngoại tiếp của tam giác SAB, ∆ cắt d.
=> $SG = frac{1}{sqrt{3}}; GI = HM = frac{1}{2}AC = frac{1}{2}$.
=> $R = SI = sqrt{frac{1}{3} + frac{1}{4}} = frac{sqrt{21}}{6}$.
Nắm vững các công thức và phương pháp giải trên, bạn sẽ tự tin chinh phục mọi bài toán liên quan đến mặt cầu ngoại tiếp hình chóp trong các kỳ thi. Chúc bạn thành công!

